Chiếu một tia sáng lên một bề mặt phẳng phản xạ ánh sáng, ta thu được một tia phản xạ tạo với tia tới một góc \({40^0}\). Giá trị của góc tới là:
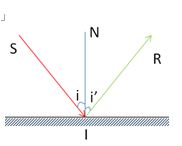
+ Ta có: \(\widehat {SIR} = i + i' = {40^0}\)
+ Áp dụng định luật phản xạ ánh sáng: \(i = i'\)
Ta suy ra: \(i = i' = \frac{{{{40}^0}}}{2} = {20^0}\)
Một tia sáng truyền đến mặt gương và có tia phản xạ như hình vẽ.
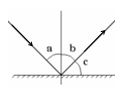
Nếu góc \(a = {45^0}\) thì:
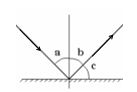
Theo định luật phản xạ ánh sáng, ta có: \(\widehat a = \widehat b = {45^0}\)
Từ hình, ta có, \(\widehat c = {90^0} - \widehat b = {90^0} - {45^0} = {45^0}\)
Một người nhìn xuống mặt hồ và thấy đỉnh ngọn cây. Hình vẽ nào sau đây mô tả đúng đường đi của tia sáng đến mắt ta?
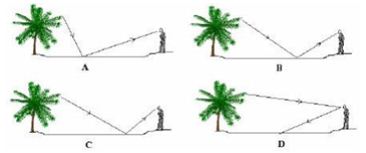
Ta có, mặt hồ đóng vai trò là một gương phẳng
Áp dụng định luật phản xạ, ta có: góc tới bằng góc phản xạ
Vẽ pháp tuyến trên các hình ta được:
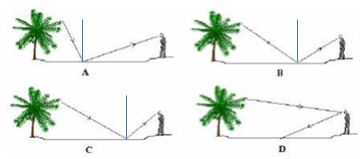
A, C – loại vì góc tới không bằng góc khúc xạ
D – loại vì đường truyền của tia sáng sai
Một tia sáng chiếu tới gương phẳng và hợp với mặt gương một góc \({30^0}\) thì góc hợp bởi tia tới và tia phản xạ là:
Ta có:
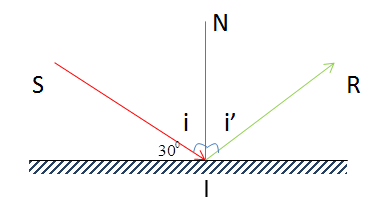
Từ hình, ta suy ra góc tới \(i = {90^0} - {30^0} = {60^0}\)
Theo định luật phản xạ ánh sáng, ta có: \(i = i' = {60^0}\)
=> Góc hợp bởi tia tới và tia phản xạ: \(\widehat {S{\rm{IR}}} = i + i' = {60^0} + {60^0} = {120^0}\)
Trong các vật sau đây, vật nào có thể được coi là một gương phẳng?
Ta có thể coi mặt phẳng của một tấm kim loại nhẵn bóng như một gương phẳng.
Một tia sáng \(SI\) truyền theo phương hợp mới mặt phẳng nằm ngang một góc \({50^0}\). Hỏi phải đặt gương phẳng hợp với mặt phẳng nằm ngang một góc bao nhiêu để tia phản xạ có phương nằm ngang.
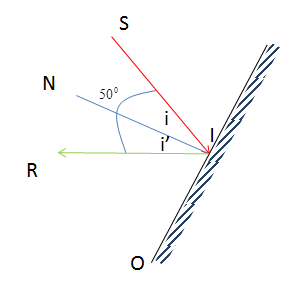
Theo đề bài, ta có: \(\widehat {SIR} = {50^0}\)
Mặt khác, theo định luật phản xạ ánh sáng, ta có: \(i = i' \leftrightarrow \widehat {SIN} = \widehat {N{\rm{IR}}} = \dfrac{{\widehat {S{\rm{IR}}}}}{2} = \dfrac{{{{50}^0}}}{2} = {25^0}\)
Góc gương cần quay so với mặt phẳng ngang để thu được tia phản xạ có phương nằm ngang chính là góc \(\widehat {RIO}\)
Ta có, \(\widehat {RIO} = \widehat {NIO} - \widehat {NIR} = {90^0} - {25^0} = {65^0}\)
Tia sáng Mặt Trời chiếu xiên hợp với mặt ngang một góc \({36^0}\) đến gặp gương phẳng cho tia phản xạ có phương thẳng đứng xuống dưới. Góc hợp bởi mặt gương và đường thẳng đứng là:
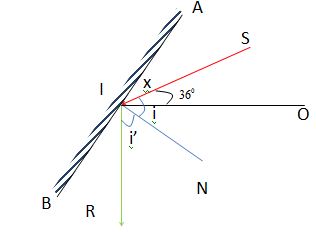
Ta có:
+ \(\widehat {RIN} = \widehat {AIO}\) (cùng phụ với \(\widehat {NIO}\)) (1)
+ Theo định luật phản xạ ánh sáng, ta có: \(i = i' \leftrightarrow \widehat {RIN} = \widehat {{\rm{NIS}}}\) (2)
Từ (1) và (2), ta suy ra: \(\widehat {AIO} = \widehat {NIS}\)
Ta suy ra: \(\widehat {{\rm{AIS}}} = \widehat {NIO} = x\)
Mặt khác, ta có: \(\left\{ \begin{array}{l}\widehat {B{\rm{IR}}} = {90^0} - i'\\\widehat {{\rm{AIS}}} = {90^0} - i\end{array} \right. \to \widehat {{\rm{AIS}}} = \widehat {B{\rm{IR}}} = x\)
Ta có:
\(\begin{array}{l}\widehat {AIN} = {90^0} = \widehat {{\rm{AIS}}} + \widehat {SIO} + \widehat {OIN}\\ \leftrightarrow {90^0} = x + {36^0} + x\\ \to x = {27^0}\end{array}\)
Vậy, ta suy ra: Góc hợp bởi mặt gương và đường thẳng đứng là \({27^0}\)
Chiếu một tia tới lên gương phẳng. Biết góc tới \(i = {30^0}\). Góc phản xạ bằng:
Ta có:
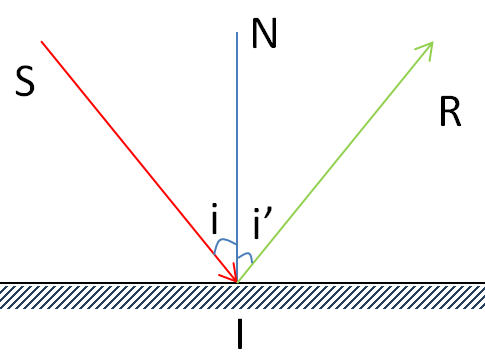
Định luật phản xạ ánh sáng:
- Tia phản xạ nằm trong mặt phẳng chứa tia tới và đường pháp tuyến của gương ở điểm tới.
- Góc phản xạ ………góc tới.
Định luật phản xạ ánh sáng:
+ Tia phản xạ nằm trong mặt phẳng chứa tia tới và pháp tuyến của gương ở điểm tới
+ Góc phản xạ bằng góc tới \(\left( {i = i'} \right)\)
Xác định vị trí của pháp tuyến tại điểm tới đối với gương phẳng?
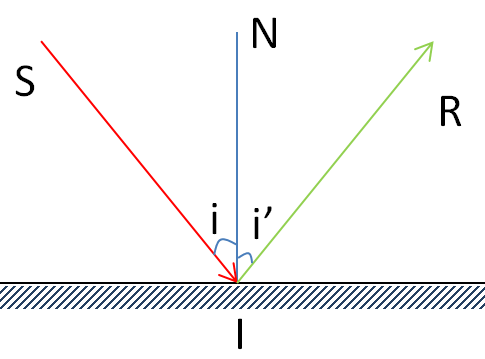
\(SI\) - tia tới
\(IR\) - tia phản xạ
\(IN\) - pháp tuyến

