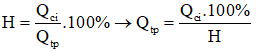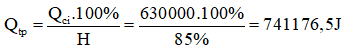Một bếp điện loại 220V - 1000W được sử dụng với hiệu điện thế 220V để đun sôi 2 l nước có nhiệt độ ban đầu 25oc. Hiệu suất của quy trình đun là 85%.

a. Tính thời gian đun sôi nước, biết nhiệt dung riêng của nước 4200 J/kg.K.

b. Mỗi ngày đun sôi 41 nước bằng bếp điện trên đây cùng với điều kiện đã cho, thì trong 1 tháng (30 ngày) phải trả bao nhiêu tiền điện cho việc đun nước này? Cho rằng giá điện là 700 đồng mỗi kW.h.

c. Nếu gập đôi dây điện trở của bếp này và vẫn sử dụng hiệu điện thế 220V thì thời gian đun sôi 21 nước có nhiệt độ ban đầu và hiệu suất như trên là bao nhiêu?

a) Nhiệt lượng cần cung cấp để đun sôi nước là:

Qcó ích = m1.c.Δtº = 2.4200.(100 – 25) = 630000 (J)

Ta có:

Nhiệt lượng do bếp điện tỏa ra là:

Vì U = Um = 220 nên bếp hoạt động với công suất P = Pm = 1000W

Ta có: Qtp = A = P.t

Thời gian đun sôi nước là: t = Qtp/P = 741176,5/1000 = 741 (s) = 12,35 phút

b) Nhiệt lượng do bếp tỏa ra để đun sôi 4 lít nước là:

Q1 = 2.Qtp = 2.741176,5 = 1482353 (J) (vì m2 = 4kg = 2m1)

Nhiệt lượng do bếp điện tỏa ra trong 30 ngày là:

Q2 = 1482353.30 = 44470590 (J)

Điện năng tiêu thụ trong 1 tháng là:

A = Q2 = 44470590 J = 12,35kW.h (vì 1kW.h = 3600000J)

Tiền điện phải trả là: Tiền = A.700 = 12,35.700 = 8645 đồng

c) Do gập đôi dây điện trở nên: tiết diện dây tăng 2 lần ⇒ điện trở giảm 2 lần

và chiều dài dây giảm 2 lần ⇒ điện trở giảm 2 lần. Vậy R giảm 4 lần

Dựa vào công thức P = U2/R nên khi R giảm 4 lần thì P tăng 4 lần, khi đó:

P’ = 4.1000 = 4000 (W)

Thời gian đun sôi nước là: t’ = Qtp/P = 741176,5/4000 = 185 (s) = 3,08 phút