Vị trí ứng với góc \(\alpha  = {30^0}\)

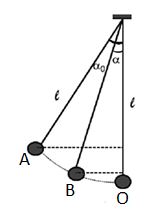
+ Chọn mốc thế năng tại vị trí cân bằng \(\left( {\alpha  = 0} \right)\)

Cơ năng tại vị trí A : ${{\rm{W}}_A} = {{\rm{W}}_{{t_A}}} = mgl\left( {1 - c{\rm{os}}{\alpha _0}} \right)$

Cơ năng tại vị trí B : ${{\rm{W}}_B} = {{\rm{W}}_{{t_B}}} + {{\rm{W}}_{{d_B}}} = mgl\left( {1 - c{\rm{os}}\alpha } \right) + \dfrac{1}{2}m{v^2}$

+ Áp dụng định luật bảo toàn cơ năng, ta có :

$\begin{array}{l}{{\rm{W}}_A} = {{\rm{W}}_B} \leftrightarrow mgl\left( {1 - c{\rm{os}}{\alpha _0}} \right) = mgl\left( {1 - c{\rm{os}}\alpha } \right) + \dfrac{1}{2}m{v^2}\\ \to v = \sqrt {2gl\left( {{\rm{cos}}\alpha  - {\rm{cos}}{\alpha _0}} \right)} \end{array}$

Thay \(\left\{ \begin{array}{l}{\alpha _0} = {45^0}\\\alpha  = {30^0}\\g = 10m/{s^2}\\l = 1m\end{array} \right.\)

Ta được : \(v = \sqrt {2.10.1.\left( {{\rm{cos3}}{{\rm{0}}^0} - c{\rm{os4}}{{\rm{5}}^0}} \right)}  \approx 1,783m/s\)