Câu hỏi:
2 năm trước
Vật nặng \(m = 2,5kg\) chuyển động thẳng đều trên mặt phẳng ngang nhờ hai dây kéo nằm trong mặt phẳng ngang và hợp với nhau góc \(\alpha = {60^0}\) không đổi. Lực kéo đặt vào mỗi dây là \(F = 10N\), lấy \(g = 9,8m/{s^2}\). Hệ số ma sát giữa vật và mặt phẳng ngang có giá trị là:
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có, các lực tác dụng lên vật được biểu diễn trong hình
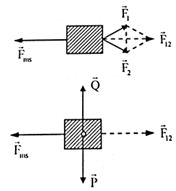
+ Mặt khác, vật chuyển động thẳng đều khi tổng hợp lực tác dụng lên vật bằng 0
ta suy ra: \[\overrightarrow {{F_{m{\rm{s}}}}} + \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow P + \overrightarrow Q = \overrightarrow 0 \](1)
Chiếu (1) ta được:
- \(Q = P\)
- \({F_{12}} = {F_{m{\rm{s}}}}\)
Ta có, \({F_1} = {F_2} = F \to {F_{12}} = 2Fc{\rm{os}}\frac{\alpha }{2}\)
Ta suy ra: \({F_{m{\rm{s}}}} = 2Fc{\rm{os}}\frac{\alpha }{2} = 2.10.c{\rm{os}}\frac{{{{60}^0}}}{2} = 10\sqrt 3 N\)
Ta lại có:
\(\begin{array}{l}{F_{m{\rm{s}}}} = \mu mg = 10\sqrt 3 N\\ \to \mu = \frac{{10\sqrt 3 }}{{2,5.9,8}} \approx 0,71\end{array}\)
Hướng dẫn giải:
+ Phân tích các lực tác dụng lên vật
+ Vận dụng điều kiện của vật chuyển động thẳng đều
Câu hỏi khác
- Đề kiểm tra 1 tiết chương 3: tĩnh học vật rắn - đề số 03 Lý 10 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 3: tĩnh học vật rắn - đề số 02 Lý 10 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 3: tĩnh học vật rắn - đề số 01 Lý 10 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 3: tĩnh học vật rắn - đề số 02 Lý 10 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 3: tĩnh học vật rắn - đề số 01 Lý 10 có lời giải chi tiết
