Câu hỏi:
2 năm trước
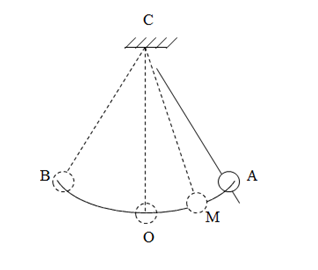
Từ điểm A của một mặt bàn phẳng nghiêng, người ta thả một vật có khối lượng \(m = 0,2kg\) trượt không ma sát với vận tốc ban đầu bằng 0 rơi xuống đất. Cho \(AB = 50cm\), \(BC = 100cm\), \(AD = 130cm\), \(g = 10m/{s^2}\). Bỏ qua lực cản không khí. Vận tốc của vật tại điểm B có giá trị là?
Trả lời bởi giáo viên
Đáp án đúng: a
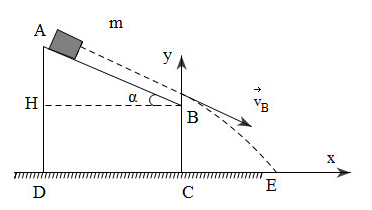
Chọn mốc thế năng tại mặt đất
Vì bỏ qua ma sát nên cơ năng của vật được bảo toàn
Ta có:
+ Cơ năng của vật tại A: ${{\rm{W}}_A} = mgAD$ (động năng của vật bằng 0 vì \({v_0} = 0\))
+ Cơ năng của vật tại B: ${{\rm{W}}_B} = \dfrac{1}{2}mv_B^2 + mgBC$
Áp dụng định luật bảo toàn cơ năng, ta có cơ năng của vật tại A bằng cơ năng của vật tại B
$\begin{array}{l}{{\rm{W}}_A} = {{\rm{W}}_B} \leftrightarrow mg.AD = \dfrac{1}{2}mv_B^2 + mg.BC\\ \leftrightarrow g.AD = \dfrac{1}{2}v_B^2 + g.BC\\ \leftrightarrow 10.1,3 = \dfrac{1}{2}v_B^2 + 10.1\\ \to {v_B} = \sqrt 6 \approx 2,45m/s\end{array}$
Hướng dẫn giải:
+ Sử dụng biểu thức tính thế năng: ${{\rm{W}}_t} = mgh$
+ Sử dụng biểu thức tính động năng: ${{\rm{W}}_d} = \dfrac{1}{2}m{v^2}$
+ Áp dụng định luật bảo toàn cơ năng
Câu hỏi khác
- Đề kiểm tra 15 phút chương 4: các định luật bảo toàn - đề số 3 Lý 10 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 4: các định luật bảo toàn - đề số 4 Lý 10 có lời giải chi tiết
- Kiểm tra 15 phút chương 4: Các định luật bảo toàn môn Lý lớp 10 có lời giải chi tiết
- Kiểm tra 1 tiết chương 4: Các định luật bảo toàn - Đề số 1 môn Lý lớp 10 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 4: các định luật bảo toàn - đề số 2 Lý 10 có lời giải chi tiết
