Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn đặt tại hai điểm \(A,B\) ở mặt nước dao động điều hòa cùng tần số, cùng pha. Hai điểm cực tiểu liên tiếp trên đoạn \(AB\) cách nhau \(2\;{\rm{cm}}\). Khoảng cách giữa hai nguồn là \(AB = 30\;{\rm{cm}}\). Xét các phần tử nước nằm trên trung trực của \(AB,\,\,{M_1},\,\,{M_2},\,\,{M_3}\) theo thứ tự đó là ba điểm liên tiếp mà phần tử mặt nước ở đó dao động cùng pha với nguồn. Khoảng cách lớn nhất giữa \({M_1}\) và \({M_3}\) gần nhất với giá trị nào sau đây?

Hai điểm cực tiểu liên tiếp trên đoạn \(AB\) cách nhau \(2\;{\rm{cm}}\)\( \Rightarrow \frac{\lambda }{2} = 2 \Rightarrow \lambda  = 4cm.\)

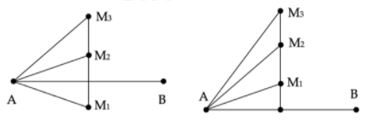
Trên trung trực của \(AB\) có 3 điểm liên liếp \({M_1},\,\,{M_2},\,\,{M_3}\) dao động cùng pha với nguồn và cách nhau xa nhất như hình vẽ.

Để \(M\) cùng pha nguồn thì:

\(AM = k\lambda  \ge \frac{{AB}}{2} \Leftrightarrow k.4 \ge 15 \Rightarrow k \ge 3,74 \Rightarrow {k_{\min  = 4}}\)

TH1: \({M_1},\,\,{M_2}\) cùng phía với \(AB\) thì lần lượt có \(k = 4,\,5,\,\,6\)

Khoảng cách lớn nhất giữa \({M_1}\) và \({M_3}\) khi này là:

\(\begin{array}{l}{M_1}{M_3} = \sqrt {AM_3^2 - {{\left( {\frac{{AB}}{2}} \right)}^2}}  - \sqrt {AM_1^2 - {{\left( {\frac{{AB}}{2}} \right)}^2}} \\ \Rightarrow {M_1}{M_3} = \sqrt {{{24}^2} - {{15}^2}}  - \sqrt {{{16}^2} - {{15}^2}}  \approx 13,2\left( {cm} \right)\end{array}\)

TH2: \({M_1},\,\,{M_2}\)khác phía với \(AB\) thì \({M_1}\)và \({M_2}\) đều có \(k = 4\) và \({M_3}\) có \(k = 5.\)

Khoảng cách lớn nhất giữa \({M_1}\) và \({M_3}\) khi này là:

\(\begin{array}{l}{M_1}{M_3} = \sqrt {AM_1^2 - {{\left( {\frac{{AB}}{2}} \right)}^2}}  + \sqrt {AM_3^2 - {{\left( {\frac{{AB}}{2}} \right)}^2}} \\ \Rightarrow {M_1}{M_3} = \sqrt {{{16}^2} - {{15}^2}}  + \sqrt {{{24}^2} - {{15}^2}}  \approx 18,8\left( {cm} \right)\end{array}\)