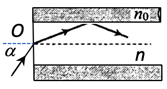
Trong sợi quang hình trụ gồm phần lõi có chiết suất \(n=1,60\) và phần vỏ bọc có chiết suất \({n_0} = 1,41\). Trong không khí, một tia sáng tới mặt trước của sợi quang tại điểm O (O nằm trên trục của sợi quang) với góc tới \(\alpha \) rồi khúc xạ vào phần lõi (như hình bên). Để tia sáng chỉ truyền đi trong phần lõi thì giá trị lớn nhất của góc \(\alpha \) gần nhất với giá trị nào sau đây?
Trả lời bởi giáo viên
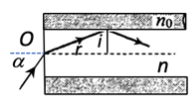
Ta có: \(\sin \alpha = n.\sin \,r \Rightarrow \sin \,r = \dfrac{{\sin \alpha }}{n}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \,\,\left( 1 \right)\)
Lại có: \(r + i = {90^0} \Rightarrow \sin i = \cos \,r\)
Để xảy ra phản xạ toàn phần tại mặt phân cách phần lõi và vỏ thì:
\(\begin{array}{l}
i \ge {i_{gh}} \Rightarrow \sin i \ge \dfrac{{{n_0}}}{n}\\
\Rightarrow \cos r \ge \dfrac{{{n_0}}}{n}{\mkern 1mu} \Leftrightarrow \sqrt {1 - {{\sin }^2}r} \ge \dfrac{{{n_0}}}{n}\,\,\,\,\left( 2 \right)
\end{array}\)
Từ (1) và (2) suy ra:
\(\begin{array}{l}
\sqrt {1 - {{\left( {\dfrac{{\sin \alpha }}{n}} \right)}^2}} \ge \dfrac{{{n_0}}}{n} \Leftrightarrow {n^2} - {\sin ^2}\alpha \ge n_0^2\\
\Leftrightarrow {\sin ^2}\alpha \le {n^2} - n_0^2\\
\Leftrightarrow \sin \alpha \le \sqrt {1,{6^2} - 1,{{41}^2}} \Rightarrow \alpha \le 49,{134^0}\\
\Rightarrow {\alpha _{\max }} = 49,{134^0}
\end{array}\)
Hướng dẫn giải:
Định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\)
Điều kiện xảy ra hiện tượng phản xạ toàn phần: \(i \ge {i_{gh}};\sin {i_{gh}} = \dfrac{{{n_2}}}{{{n_1}}}\)