Câu hỏi:
2 năm trước
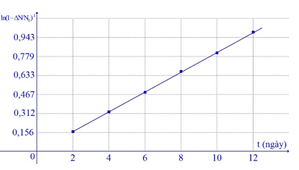
Trong phòng thí nghiệm, người ta tiến hành xác định chu kì bán rã \(T\) của một chất phóng xạ bằng cách dùng máy đếm xung để đo tỉ lệ giữa số hạt bị phân rã \({\rm{\Delta N}}\) và số hạt ban đầu \({{\rm{N}}_{\rm{0}}}{\rm{.}}\) Dựa vào kết quả thực nghiệm đo được trên đồ thị hãy tính chu kì bán rã của chất phóng xạ này?
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có: \(N = {N_0}{e^{ - \lambda t}} \Rightarrow \)Số hạt bị phân rã là:
\(\Delta N = {N_0} - {N_0}{e^{ - \lambda t}} = {N_0}(1 - {e^{ - \lambda t}})\)
\( \Rightarrow \dfrac{{\Delta N}}{{{N_0}}} = 1 - {e^{ - \lambda t}} \Rightarrow 1 - \dfrac{{\Delta N}}{{{N_0}}} = {e^{ - \lambda t}}\)
\( \Rightarrow \dfrac{1}{{\left( {1 - \dfrac{{\Delta N}}{{{N_0}}}} \right)}} = {e^{\lambda t}} \Rightarrow \ln {\left( {1 - \dfrac{{\Delta N}}{{{N_0}}}} \right)^{ - 1}} = \lambda t\)
Từ đồ thị ta thấy \(\lambda \approx 0,078\)
\( \Rightarrow T = \dfrac{{\ln 2}}{\lambda } \approx 8,9\) (ngày)
Hướng dẫn giải:
Áp dụng công thức tính số hạt còn lại trong mẫu sau thời gian t là:
\(N = {N_0}{e^{ - \lambda t}} = {N_0}{2^{\dfrac{{ - t}}{T}}}\)
Câu hỏi khác
- Kiểm tra 15 phút chương 7: Hạt nhân nguyên tử - Đề số 1 môn Lý lớp 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 7: hạt nhân nguyên tử - đề số 3 Lý 12 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 7: hạt nhân nguyên tử - đề số 3 Lý 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 7: hạt nhân nguyên tử - đề số 2 Lý 12 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 7: hạt nhân nguyên tử - đề số 1 Lý 12 có lời giải chi tiết
