Trả lời bởi giáo viên
Đáp án đúng: a
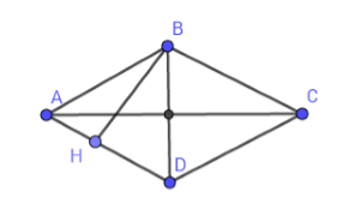
Xét hình thoi ABCD có hai đường chéo AC và BD vuông góc với nhau. Kẻ BH vuông góc với AD.
Ta có: \({S_{ABCD}} = AD.BH\)
Trong tam giác vuông ABH vuông tại H thì:
\(BH \le AB\) (đường vuông góc ngắn hơn đường xiên)
Do đó: \({S_{ABCD}} = AD.BH \le AD. AB = AB. AB = A{B^2}\).
\({S_{ABCD}}\) có giá trị lớn nhất bằng \(A{B^2}\) khi ABCD là hình vuông.
Vậy trong các hình thoi có cùng chu vi thì hình vuông có diện tích lớn nhất.
Hướng dẫn giải:
Sử dụng công thức tính diện tích hình thoi ABCD: \({S_{ABCD}} = BH.AD\) với BH là đường cao của hình thoi ứng với cạnh AD.
Theo tính chất đường xiên của tam giác ta có: \(BH \le AB\).
Câu hỏi khác
- Đề kiểm tra 15 phút chương 6: đa giác, diện tích đa giác - đề số 2 Toán 8 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 6: Đa giác, diện tích đa giác - đề số 2 Toán 8 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 6: Đa giác, diện tích đa giác - đề số 1 Toán 8 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 6: đa giác, diện tích đa giác - đề số 1 Toán 8 có lời giải chi tiết
