Câu hỏi:
2 năm trước
Tại điểm \(O\) đặt hai nguồn âm điểm giống hệt nhau phát ra âm đẳng hướng có công suất không đổi. Điểm \(A\) cách \(O\) một đoạn \(d\) (\(m\)) có mức cường độ âm là \(L_A = 40 dB\). Trên tia vuông góc với \(OA\) tại \(A\), lấy điểm \(B\) cách \(A\) một khoảng \(6 m\). Điểm \(M\) thuộc đoạn \(AB\) sao cho \(AM = 4,5 m\) và góc \(\widehat {MOB}\)có giá trị lớn nhất. Để mức cường độ âm tại \(M\) là \(50 dB\) thì cần đặt thêm tại \(O\) bao nhiêu nguồn âm nữa?
Trả lời bởi giáo viên
Đáp án đúng: d
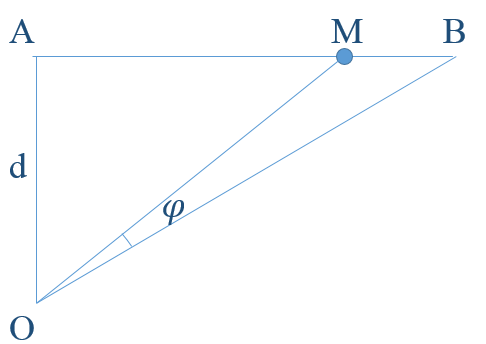
\(\tan \widehat {MOB} = \dfrac{{\tan \widehat {AOB} - \tan \widehat {AOM}}}{{1 + \tan \widehat {AOB}\tan \widehat {AOM}}} = \dfrac{{\dfrac{{AB}}{{AO}} - \dfrac{{AM}}{{AO}}}}{{1 + \dfrac{{AB}}{{AO}}.\dfrac{{AM}}{{AO}}}}\)
\( \Rightarrow \tan \varphi = \dfrac{{\dfrac{{AB}}{d} - \dfrac{{AM}}{d}}}{{1 + \dfrac{{AB}}{d}.\dfrac{{AM}}{d}}} = \dfrac{{AB - AM}}{{d + \dfrac{{AB.AM}}{d}}}\)
\( \Rightarrow \tan \varphi \) đạt cực đại khi \(\left( {d + \dfrac{{AB.AM}}{d}} \right)\) đạt min \(d = \dfrac{{AB.AM}}{d} \Leftrightarrow d = \sqrt {AB.AM} = 3\sqrt 3 (m)\)
\( \Rightarrow OM = \sqrt {A{O^2} + A{M^2}} = \dfrac{{3\sqrt {21} }}{2}(m)\)
\( \Rightarrow {L_A} - {L_M} = 20\lg \dfrac{{{r_M}}}{{{r_A}}} = 2,43(dB) \Rightarrow {L_M} = 37,57(dB)\)
Để mức cường độ âm tại M là 50 dB thì:
\({L_2} - {L_1} = 10\lg \dfrac{{{P_2}}}{{{P_1}}} = 50 - 37,57 = 12,43 \Rightarrow {P_2} \approx 35P\)
Trong đó P là công suất của một nguồn âm.
Suy ra cần thêm 33 nguồn âm nữa
Hướng dẫn giải:
Ta sử dụng công thức:
\(\tan ({\varphi _2} - {\varphi _1}) = \dfrac{{\tan {\varphi _2} - \tan {\varphi _1}}}{{1 + \tan {\varphi _2}\tan {\varphi _1}}}\), góc MOB có giá trị lớn nhất khi tan MOB lớn nhất
Câu hỏi khác
- Đề thi thử thpt qg sở gdđt hà nội - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg trường thpt chuyên lam sơn - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg sở gdđt kiên giang - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg - đề số 01 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg trường thpt kim liên (2021) Lý 12 có lời giải chi tiết
