Ở mặt nước, tại hai điểm A và B cách nhau \(8cm\) có hai nguồn giống nhau dao động theo phương thẳng đứng, phát ra hai sóng có bước sóng \(1cm\). M, N là hai điểm thuộc mặt nước cách nhau \(4cm\) và ABMN là hình thang cân (AB // MN). Để trong đoạn MN có đúng \(5\) điểm dao động với biên độ cực đại thì diện tích lớn nhất của hình thang có giá trị nào sau đây?
Trả lời bởi giáo viên
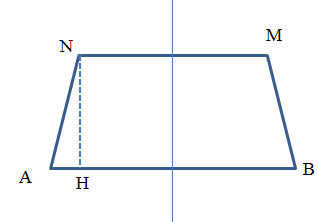
Để trên MN có đúng 5 điểm cực đại thì M và N nằm trên các đường cực đại bậc 2
NB – NA = 2λ = 2cm
\( \Rightarrow \sqrt {H{B^2} + N{H^2}} - \sqrt {H{A^2} + N{H^2}} = 2 \\\Rightarrow \sqrt {{6^2} + N{H^2}} - \sqrt {{2^2} + N{H^2}} = 2cm \\\Rightarrow NH = 3\sqrt{5} cm\)
Diện tích hình thang :
\(S = \dfrac{{AB + MN}}{2}.NH = \dfrac{{8 + 4}}{2}.3\sqrt{5}=18\sqrt 5 c{m^2}\)
Hướng dẫn giải:
Tại M dao động cực đại nên d2 – d1 = kλ