Ở bề mặt một chất lỏng có hai nguồn phát sóng kết hợp \({S_1}\) và \({S_2}\) cách nhau \(15cm\). Hai nguồn này dao động theo phương thẳng đứng có phương trình lần lượt là \({u_1} = 5cos50\pi t\left( {mm} \right)\) và \({u_2} = 5cos(50\pi t + \pi ){\rm{ }}\left( {mm} \right)\). Tốc độ truyền sóng trên mặt chất lỏng là \(120cm/s\). Xét các điểm trên \({S_1}{S_2}\). Gọi I là trung điểm của \({S_1}{S_2}\); M nằm cách I một đoạn 3cm sẽ dao động với biên độ:
Trả lời bởi giáo viên
Cách 1:
+ Bước sóng: \(\lambda = \frac{v}{f} = \frac{{120}}{{\frac{{50\pi }}{{2\pi }}}} = 4,8cm\)
+ Ta có biên độ dao động tại một điểm bất kì trong trường giao thoa:
\(a = 2A\left| {c{\rm{os}}\left( {\pi \frac{{{d_1} - {d_2}}}{\lambda } + \frac{\pi }{2}} \right)} \right| = 10c{\rm{os}}\left( {\pi \frac{{{d_1} - {d_2}}}{\lambda } + \frac{\pi }{2}} \right)\)
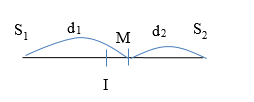
Ta có: \({d_2} - {\rm{ }}{d_1} = {\rm{ }}2MI{\rm{ }} = {\rm{ }}6cm\)
\( \to {a_M} = 10\left| {c{\rm{os}}\left( {\pi \frac{6}{{4,6}} + \frac{\pi }{2}} \right)} \right| = 10\left| {cos\left( {\frac{{7\pi }}{4}} \right)} \right| = 5\sqrt 2 mm\)
Hướng dẫn giải:
- Áp dụng công thức tính bước sóng: \(\lambda = \frac{v}{f}\)
- Sử dụng công thức tính biên độ tại 1 điểm bất kì trong trường giao thoa với 2 nguồn ngược pha nhau: \(a = 2A\left| {c{\rm{os}}\left( {\pi \frac{{{d_1} - {d_2}}}{\lambda } + \frac{\pi }{2}} \right)} \right|\)