Một viên đạn khối lượng 1kg đang bay theo phương thẳng đứng với vận tốc 500m/s thì nổ thành hai mảnh có khối lượng bằng nhau. Mảnh thứ nhất bay theo phương ngang với vận tốc \(500\sqrt 2 m/s\). Hỏi mảnh thứ 2 bay theo phương nào với vận tốc bao nhiêu?
Trả lời bởi giáo viên
\(\begin{array}{l}m = 1kg;v = 500m/s\\{m_1} = {m_2} = \dfrac{m}{2} = 0,5kg;{v_1} = 500\sqrt 2 m/s\end{array}\)
Xét hệ gồm hai mảnh đạn trong thời gian nổ.
Động lượng của hệ trước khi đạn nổ: \(\overrightarrow p = m.\overrightarrow v \)
Động lượng sau khi đạn nổ: \(\overrightarrow {p'} = \overrightarrow {{p_1}} + \overrightarrow {{p_2}} = {m_1}.\overrightarrow {{v_1}} + {m_2}.\overrightarrow {{v_2}} \)
Áp dụng định luật bảo toàn động lượng ta có: \(\overrightarrow p = \overrightarrow {p'} \Rightarrow \overrightarrow p = \overrightarrow {{p_1}} + \overrightarrow {{p_2}} \)
Viên đạn đang bay theo phương thẳng đứng thì nổ thành hai mảnh mảnh thứ nhất bay theo phương ngang. Ta có hình vẽ:
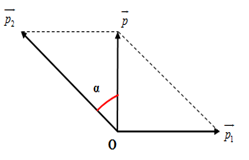
Từ hình vẽ ta có:
\(\begin{array}{l}p_2^2 = {p^2} + p_1^2 \Leftrightarrow {\left( {\dfrac{m}{2}.{v_2}} \right)^2} = {\left( {mv} \right)^2} + {\left( {\dfrac{m}{2}.{v_1}} \right)^2}\\ \Rightarrow v_2^2 = 4{v^2} + v_1^2 = {4.500^2} + {\left( {500\sqrt 2 } \right)^2} \Rightarrow {v_2} = 1225m/s\end{array}\)
Góc hợp bởi giữa \(\overrightarrow {{v_2}} \) và phương thẳng đứng là : \(\sin \alpha = \dfrac{{{p_1}}}{{{p_2}}} = \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{500\sqrt 2 }}{{1225}} \Rightarrow \alpha = {35^0}\)
Hướng dẫn giải:
Động lượng của một vật khối lượng m đang chuyển động với vận tốc \(\overrightarrow v \) là đại lượng được xác định bởi công thức: \(\overrightarrow p = m\overrightarrow v \)
Định luật bảo toàn động lượng: Động lượng của một hệ cô lập là một đại lượng bảo toàn

