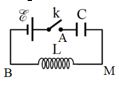
Một mạch dao động \(LC\) lí tưởng được mắc với nguồn điện có suất điện động \(6\;V\), điện trở trong không đáng kể (hình vẽ bên). Điện dung của tụ điện là \(0,5\mu F;\) độ tự cảm của cuộn dây là \(2mH\). Lấy \({\pi ^2} = 10.\) Ban đầu khóa \({\rm{k}}\) ngắt tụ điện chưa tích điện, tại thời điểm \(t = 0\) người ta đóng khóa \({\rm{k}}\) thì trong mạch có dao động điện từ tự do. Kể từ \(t = 0\), thời điểm mà cường độ dòng điện trong mạch có độ lớn \(15\sqrt 3 \pi ({\rm{mA}})\) lần thứ 3 thì điện tích của bản tụ điện nối với khóa \({\rm{k}}\) có giá trị là

Bản chất của tia phóng xạ \(\alpha \) là

Đặt điện áp xoay vào hai đầu đoạn mạch gồm điện trở thuần \(R = 40\Omega \) mắc nối tiếp với tụ điện thì dung kháng của tụ điện là \({Z_C} = 60\Omega \). Tổng trở của đoạn mạch là

Xét nguyên tử hiđrô theo mẫu nguyên tử Bo, mức năng lượng của nó ở các trạng thái dừng theo thứ tự tăng dần từ giá trị nhỏ nhất là \({E_1},{E_2},{E_3} \ldots \) Nguyên tử hiđrô hấp thụ một phôtôn có năng lượng \(\varepsilon  = {E_3} - {E_1}\) thì êlectron chuyển từ quỹ đạo

Một sóng ngang truyền trên sợi dây rất dài với phương trình sóng \(u = A\cos \left( {20\pi t - \frac{\pi }{{10}}x} \right)\) (\(x\) tính bằng \({\rm{cm}},t\) tính bằng \({\rm{s}})\). Bước sóng trên sợi dây là

Giới hạn quang điện của kim loại đồng là \(0,3\mu m\). Chiếu lần lượt các bức xạ có bước sóng (trong chân không) là \(0,50\mu m;\,\,0,28\mu m;\,\,0,35\mu m;\,\,0,41\mu m\) và \(0,19\mu m\) vào một tấm đồng. Số bức xạ gây ra được hiện tượng quang điện ngoài là

Khoảng cách từ đài truyền hình Việt Nam (VTV) đến vệ tinh VINASAT-2 khoảng \(36.000\;{\rm{km}}\). Cho \(c = {3.10^8}\;m/s\). Thời gian để sóng vô tuyến truyền từ đài VTV đến vệ tinh có giá trị là

Cấu tạo của buồng tối trong máy quang phổ lăng kính gồm