Một lượng khí biến đổi theo chu trình biểu diễn bởi đồ thị.

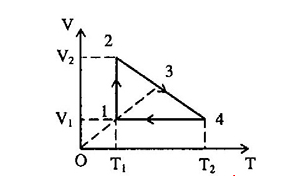
Cho biết ${p_1} = {p_3}$, ${V_1} = 1{m^3}$, ${V_2} = 4{m^3}$, ${T_1} = 100K$, ${T_4} = 300K$. Tìm giá trị của ${V_3}$?

Ta có:

- Quá trình $\left( 1 \right) \to \left( 2 \right)$: Quá trình đẳng nhiệt: ${T_2} = {T_1} = 100K$ , ${V_2} = 4{m^3}$

- Quá trình $\left( 4 \right) \to \left( 1 \right)$: Quá trình đẳng tích: ${V_4} = {V_1} = 1{m^3}$, ${T_4} = 300K$

- Qúa trình $\left( 2 \right) \to \left( 4 \right)$: $V = aT + b$

+ Trạng thái 2: $4 = 100a + b$ (1)

+ Trạng thái 4: $1 = 300a + b$ (2)

Từ $\left( 1 \right),\left( 2 \right)$ ta suy ra: $\left\{ \begin{array}{l}a =  - \dfrac{3}{{200}}\\b = \dfrac{{11}}{2}\end{array} \right.$

$\Rightarrow V =  - \dfrac{3}{{200}}T + \dfrac{{11}}{2}$  (3)

- Quá trình $\left( 1 \right) \to \left( 3 \right)$: Quá trình đẳng áp $V = \dfrac{{{V_1}}}{{{T_1}}}T = \dfrac{1}{{100}}T$  (4)

Vì $\left( 3 \right)$ là giao điểm của 2 đường $\left( 2 \right) \to \left( 4 \right)$ và $\left( 1 \right) \to \left( 3 \right)$ nên:

$\begin{array}{l} - \dfrac{3}{{200}}{T_3} + \dfrac{{11}}{2} = \dfrac{1}{{100}}{T_3}\\ \Rightarrow {T_3} = 220K\end{array}$

Thay vào (4) suy ra ${V_3} = \dfrac{{220}}{{100}} = 2,2{m^3}$