Câu hỏi:
2 năm trước
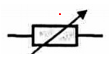
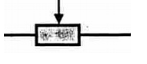
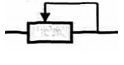
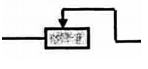
Một đoạn mạch gồm ba điện trở \({R_1} = 9\Omega ,{R_2} = 18\Omega \) và \({R_3} = 24\Omega \) được mắc vào hiệu điện thế $U = 3,6V$ như sơ đồ bên
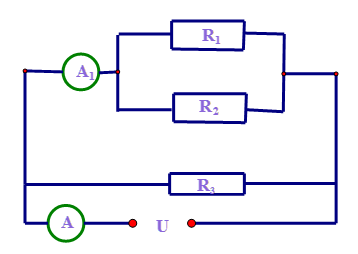
Số chỉ của ampe kế A và A1 là:
Trả lời bởi giáo viên
Đáp án đúng: c
+ Điện trở tương đương của đoạn mạch gồm \({R_1}\) và \({R_2}\) mắc song song là \({{\rm{R}}_{{\rm{12}}}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \dfrac{{9.18}}{{9 + 18}} = 6\Omega \)
Điện trở tương đương của đoạn mạch là \({{\rm{R}}_{{\rm{123}}}} = \dfrac{{{R_{12}}{R_3}}}{{{R_{12}} + {R_3}}} = \dfrac{{6.24}}{{6 + 24}} = 4,8\Omega \)
+ Số chỉ của ampe kế A là \(I = \dfrac{U}{{{R_{123}}}} = \dfrac{{3,6}}{{4,8}} = 0,75{\rm{A}}\)
Số chỉ của ampe kế A1 là \({{\rm{I}}_{\rm{1}}} = \dfrac{U}{{{R_{12}}}} = \dfrac{{3,6}}{6} = 0,6{\rm{A}}\)
Hướng dẫn giải:
+ Sử dụng biểu thức tính điện trở tương đương trong đoạn mạch có các điện trở mắc song song:
\(\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ...\)
+ Áp dụng biểu thức định luật Ôm tính cường độ dòng điện: \(I = \dfrac{U}{R}\)
Câu hỏi khác
- Đề kiểm tra giữa học kì 1 - đề số 01 Lý 9 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 02 Lý 9 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 03 Lý 9 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 4 Lý 9 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 01 Lý 9 có lời giải chi tiết
