Câu hỏi:
1 năm trước
Một con lắc đơn gồm vật nặng \(m = 400g\), dây treo không dãn có chiều dài \(l = 1,5m\). Chọn mốc thế năng tại vị trí cân bằng của vật, lấy \(g = 10m/{s^2}\), ở góc lệch \(\alpha = {60^0}\) so với phương thẳng đứng vật có thế năng \({{\rm{W}}_t}\). Cơ năng của vật có giá trị:
Trả lời bởi giáo viên
Đáp án đúng: d
- Chọn mốc tính thế năng tại vị trí thấp nhất của vật
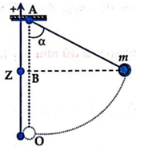
Thế năng của vật là: \({{\rm{W}}_t} = mg{\rm{z}}\)
Từ hình ta có: \(z = OB = OA - AB = l - lco{\rm{s}}\alpha = l\left( {1 - co{\rm{s}}\alpha } \right)\)
Từ đó cơ năng của vật tại vị trí ứng với \(\alpha = {60^0}\) là:
\(\begin{array}{l}{{\rm{W}}_t} = mg{\rm{z = mgl}}\left( {1 - co{\rm{s}}\alpha } \right)\\ \Rightarrow {{\rm{W}}_t} = 0.4.10.1,5.\left( {1 - co{\rm{s}}{{60}^ \circ }} \right) = 3J\end{array}\)
Hướng dẫn giải:
Chọn mốc thế năng
Áp dụng công thức tính thế năng:
Áp dụng lý thuyết cơ năng bằng tổng động năng và thế năng
Áp dụng định luật bảo toàn cơ năng
