Câu hỏi:
2 năm trước
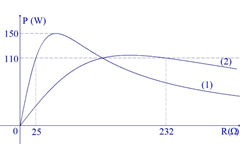
Lần lượt đặt vào hai đầu đoạn mạch xoay chiều RLC không phân nhánh (\(R\) là biến trở, \(L\) thuần cảm) hai điện áp xoay chiều \({u_1} = {U_{01}}\cos ({\omega _1}t + {\varphi _1})\) và \({u_2} = {U_{02}}\cos ({\omega _2}t + {\varphi _2})\) người ta thu được đồ thị công suất của mạch điện xoay chiều theo biến trở \(R\) như hình vẽ (đường 1 là của \(u_1\) và đường 2 là của \(u_2\)). Khi sử dụng điện áp \(u_2\) thì công suất tiêu thụ của mạch đạt giá trị lớn nhất là
Trả lời bởi giáo viên
Đáp án đúng: d
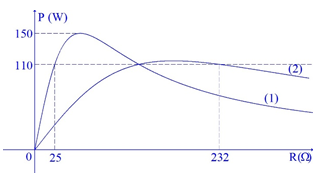
Ta có:
\({P_{1\max }} = \dfrac{{U_1^2}}{{2{R_{01}}}} = 150({\rm{W}})\); \(R_{01}^2 = {R_1}{R_2} = 25{R_2}\)
\({P_{2\max }} = \dfrac{{U_2^2}}{{2{R_{02}}}}\); \(R_{02}^2 = 232{R_2}\)
\({R_1} + {R_2} = \dfrac{{U_1^2}}{P} \Rightarrow 25 + {R_2} = \dfrac{{U_1^2}}{{110}} \Rightarrow U_1^2 = 110.\left( {25 + {R_2}} \right)\)
và \(R{'_1} + R{'_2} = \dfrac{{U_2^2}}{P} \Rightarrow {R_2} + 232 = \dfrac{{U_2^2}}{{110}} \Rightarrow U_2^2 = 110.({R_2} + 232)\)
(Lưu ý: \({R_2} = R{'_1}\))
\( \Rightarrow {P_{1\max }} = \dfrac{{U_1^2}}{{2{R_{01}}}} = \dfrac{{110.\left( {25 + {R_2}} \right)}}{{2\sqrt {25{R_2}} }} = 150 \Rightarrow {150^2}.100{R_2} = {110^2}{(25 + {R_2})^2} \Rightarrow {R_2} \approx 131(\Omega )\)
\({P_{2\max }} = \dfrac{{U_2^2}}{{2{R_{02}}}} = \dfrac{{110.({R_2} + 232)}}{{2\sqrt {232{R_2}} }} = 114,5({\rm{W}})\)
Hướng dẫn giải:
Sử dụng công thức: \({P_{\max }} = \dfrac{{{U^2}}}{{2{R_0}}}\) và \({R_1}{R_2} = R_0^2\)
Với R1, R2 có cùng giá trị công suất P
Câu hỏi khác
- Đề thi thử thpt qg sở gdđt hà nội - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg trường thpt chuyên lam sơn - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg sở gdđt kiên giang - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg - đề số 01 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg trường thpt kim liên (2021) Lý 12 có lời giải chi tiết
