Câu hỏi:
2 năm trước
Hai điện tích \({q_1}\; = q\)và \({q_2}\; = 4q\) đặt cách nhau một khoảng d trong không khí. Gọi M là vị trí tại đó, lực tổng hợp tác dụng lên điện tích q0 bằng 0. Điểm M cách q1 một khoảng
Trả lời bởi giáo viên
Đáp án đúng: b
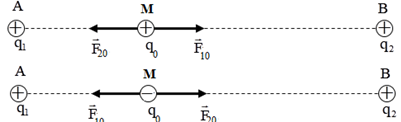
Để q0 cân bằng \( \Rightarrow \overrightarrow {{F_{10}}} + \overrightarrow {{F_{20}}} = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{F_{10}}} \, \uparrow \downarrow \,\overrightarrow {{F_{20}}} \,\,\,\left( 1 \right)\\{F_{10}} = {F_{20}}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Do \({q_1};{q_2}\) cùng dấu → Để lực tổng hợp tại M bằng 0 thì M nằm trên đường nối q1, q2 và nằm trong khoảng q1, q2 \( \Rightarrow {r_1} + {r_2} = d\,\,\,\left( * \right)\)
Lại có: \({F_{10}} = {F_{20}} \Leftrightarrow \dfrac{{k\left| {{q_1}{q_0}} \right|}}{{r_1^2}}\, = \,\dfrac{{k\left| {{q_2}{q_0}} \right|}}{{r_2^2}}\)
\( \Leftrightarrow \dfrac{{\left| {{q_1}} \right|}}{{\left| {{q_2}} \right|}}\, = \dfrac{{r_1^2}}{{r_2^2}} = \dfrac{q}{{4q}}\, = \dfrac{1}{4} \Leftrightarrow \dfrac{{{r_1}}}{{{r_2}}} = \dfrac{1}{2} \Rightarrow 2{r_1} = {r_2}\,\,\left( {**} \right)\)
Từ (*) và (**) ta có: \(\left\{ \begin{array}{l}{r_1} + {r_2} = d\,\\2{r_1} = {r_2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{r_1} = \dfrac{d}{3}\\{r_2} = \dfrac{{2d}}{3}\end{array} \right.\)
Hướng dẫn giải:
Để \({q_0}\) cân bằng thì:
\(\overrightarrow {{F_{10}}} + \overrightarrow {{F_{20}}} = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{F_{10}}} \, \uparrow \downarrow \,\overrightarrow {{F_{20}}} \,\,\,\left( 1 \right)\\{F_{10}} = {F_{20}}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Giải (1) \( \Rightarrow \) ba điện tích thẳng hàng
+ Nếu \({q_1};{q_2}\) cùng dấu \( \Rightarrow \) q0 nằm trong q1 và q2.
(Không phụ thuộc vào dấu của q0)
+ Nếu \({q_1};{q_2}\) trái dấu \( \Rightarrow \) q0 nằm ngoài q1 và q2 và gần điện tích có độ lớn nhỏ hơn.
(Không phụ thuộc vào dấu của q0)
Câu hỏi khác
- Đề kiểm tra giữa học kì 2 - đề số 1 Lý 11 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 4 Lý 11 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 1 Lý 11 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 05 Lý 11 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 04 Lý 11 có lời giải chi tiết
