Câu hỏi:
2 năm trước
Dùng một proton có động năng \(5,45 MeV\) bắn vào hạt nhân \({}_4^9Be\) đang đứng yên. Phản ứng tạo ra hạt nhân X và hạt \(α\). Hạt \(α\) bay ra theo phương vuông góc với phương tới của hạt proton và có động năng \(4,0 MeV\). Khi tính động năng của các hạt, lấy khối lượng các hạt nhân tính theo đơn vị khối lượng nguyên tử bằng số khối của chúng. Năng lượng tỏa ra trong phản ứng này bằng
Trả lời bởi giáo viên
Đáp án đúng: b
+ PT phản ứng: \(p + {}_4^9Be \to \alpha + {}_3^6X\)
+ Theo định luật bảo toàn động lượng ta có: \(\overrightarrow {{p_p}} = \overrightarrow {{p_\alpha }} + \overrightarrow {{p_X}} \)
=> ta biểu diễn bằng hình vẽ sau:
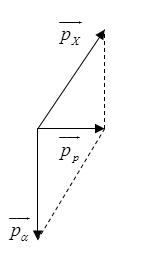
Từ hình vẽ ta có: \(p_X^2 = p_\alpha ^2 + p_p^2\)
Mà : \({p^2} = 2mK \Rightarrow {m_X}{K_X} = {m_\alpha }{K_\alpha } + {m_p}{K_p} \Rightarrow {K_X} = \dfrac{{{m_\alpha }{K_\alpha } + {m_p}{K_p}}}{{{m_X}}} = \dfrac{{4.4 + 1.5,45}}{6} = 3,575(MeV)\)
Năng lượng tỏa ra của phản ứng : \(\Delta E = {K_X} + {K_\alpha } - {K_p} = 3,575 + 4 - 5,45 = 2,125(MeV)\)
Hướng dẫn giải:
+ Sử dụng định luật bảo toàn số khối và bảo toàn điện tích để viết phương trình phản ứng.
+ Sử dụng định luật bảo toàn động lượng trong phản ứng hạt nhân.
+ Công thức liên hệ giữa động lượng và động năng: \({p^2} = {\rm{ }}2mK\)
+ Công thức tính năng lượng toả ra của phản ứng: \(\Delta E = \left( {{m_t} - {m_s}} \right){c^2} = {K_s} - {K_t}\)
(Kt, Ks lần lượt là tổng động năng của các hạt trước và sau phản ứng)
Câu hỏi khác
- Kiểm tra 15 phút chương 7: Hạt nhân nguyên tử - Đề số 1 môn Lý lớp 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 7: hạt nhân nguyên tử - đề số 3 Lý 12 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 7: hạt nhân nguyên tử - đề số 3 Lý 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 7: hạt nhân nguyên tử - đề số 2 Lý 12 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 7: hạt nhân nguyên tử - đề số 1 Lý 12 có lời giải chi tiết
