Câu hỏi:
2 năm trước
Dùng một âm thoa có tần số rung f = 100Hz người ta tạo ra hai điểm S1,S2 trên mặt nước hai nguồn sóng cùng biên độ,cùng pha.S1S2 = 3,2cm.Tốc độ truyền sóng là 40 cm/s. I là trung điểm của S1S2. Định những điểm dao động cùng pha với I.Tính khoảng từ I đến điểm M gần I nhất dao động cùng pha với I và nằm trên trung trực S1S2 là:
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có:
\(\lambda = \frac{v}{f} = 0,4cm\)
- Giả sử phương trình sóng của 2 nguồn là
\({u_{S1}} = {\rm{ }}{u_{S2}} = {\rm{ }}Acos(200\pi t)\)
- Thì phương trình sóng tại I là:
\({u_I} = {u_{1I}} + {u_{2I}} = 2A\cos (200\pi t - 2\pi \frac{{1,6}}{{0,4}}) = 2A\cos (200\pi t - 8\pi ) = 2A\cos (200\pi t)\)
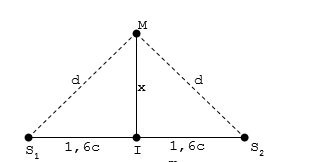
-Tương tự PT sóng tại M cách mỗi nguồn đoạn d ( như hình vẽ ) là:
\({u_M} = 2A\cos (200\pi t - 2\pi \frac{d}{{0,4}})\)
=> Độ lệch pha giữa I và M là
\(\Delta \varphi = 2\pi \frac{d}{{0,4}}\)
để I và M cùng pha thì
\(\Delta \varphi = k2\pi \to d = k.0,4(cm)\)
Theo hình vẽ dễ thấy
\(d > 1,6{\text{ }}cm \to d = k.0,4 > 1,6 \Rightarrow k > 4\)
* Mặt khác cần tìm xmin nên d cũng phải min => k cũng min => kmin=5 => dmin=5.0,4=2cm
${x_{min}} = \sqrt {d_{\min }^2 - 1,{6^2}} = 1,2cm$
Hướng dẫn giải:
+ Áp dụng biểu thức xác định bước sóng: \(\lambda = \frac{v}{f}\)
+ Viết phương trình dao động sóng
+ Áp dụng điều kiện dao động cùng pha: \(\Delta \varphi = k2\pi \)
Câu hỏi khác
- Đề kiểm tra 1 tiết chương 2: sóng cơ và sóng âm - đề số 01 Lý 12 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 2: Sóng cơ và sóng âm - Đề số 03 Lý 12 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 2: sóng cơ và sóng âm - đề số 02 Lý 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 2: Sóng cơ và sóng âm - đề số 03 Lý 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 2: Sóng cơ và sóng âm - đề số 02 Lý 12 có lời giải chi tiết
