Câu hỏi:
2 năm trước
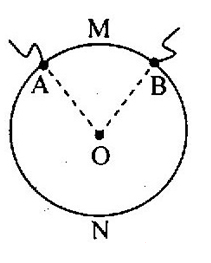
Dòng điện chạy qua một vòng dây dẫn tại hai điểm A, B. Dây dẫn tạo nên vòng dây là đồng chất, tiết diện đều và có điện trở \({R_0} = 25\Omega \), góc \(AOB = \alpha = {72^0}\). Tính điện trở tương đương của vòng dây khi mắc vào mạch điện tại A và B.
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có:
+ Điện trở của cả vòng dây là \({R_0}\)
+ Chiều dài của vòng dây là \(C = 2\pi r\) (với \(r\) là bán kính của vòng tròn)
+ Điện trở của đoạn \(AMB\) là: \({R_{AMB}} = \dfrac{\alpha }{{360}}{R_0}\)
+ Điện trở của đoạn \(ANB\) là: \({R_{ANB}} = \dfrac{{360 - \alpha }}{{360}}{R_0}\)
Mặt khác, ta có: \(AMB//ANB\) nên: \(R = \dfrac{{{R_{AMB}}{R_{ANB}}}}{{{R_{AMB}} + {R_{ANB}}}} = \dfrac{{\left( {360 - \alpha } \right)\alpha }}{{{{360}^2}}}{R_0}\)
Thay \(\left\{ \begin{array}{l}\alpha = {72^0}\\{R_0} = 25\Omega \end{array} \right.\) ta được: \(R = \dfrac{{\left( {360 - 72} \right).72}}{{{{360}^2}}}.25 = 4\Omega \)
Hướng dẫn giải:
+ Sử dụng biểu thức tính chu vi hình tròn: \(C = 2\pi r\)
+ Vận dụng biểu thức tính điện trở tương đương của mạch có các điện trở mắc song song: \(\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\)
Câu hỏi khác
- Đề kiểm tra giữa học kì 2 - đề số 1 Lý 11 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 4 Lý 11 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 1 Lý 11 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 05 Lý 11 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 04 Lý 11 có lời giải chi tiết
