Câu hỏi:
2 năm trước
Đoạn mạch điện xoay chiều gồm điện trở thuần R mắc nối tiếp với cuộn dây. Điện áp hiệu dụng ở hai đầu điện trở, cuộn dây và hai đầu đoạn mạch lần lượt là \(35V,85V\) và \(75\sqrt 2 V\). Cuộn dây tiêu thụ công suất \(40W\). Tổng điện trở thuần của toàn mạch có giá trị là bao nhiêu?
Trả lời bởi giáo viên
Đáp án đúng: d
Ta có:
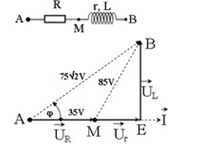
Từ giản đồ, xét tam giác MAB, có:
\(\begin{array}{l}M{B^2} = A{B^2} + A{M^2} - 2AB.AM.cos\varphi \\ \Rightarrow cos\varphi = \dfrac{{A{B^2} + A{M^2} - M{B^2}}}{{2AB.AM}}\\ = \dfrac{{{{\left( {75\sqrt 2 } \right)}^2} + {{\left( {35} \right)}^2} - {{85}^2}}}{{2.75\sqrt 2 .35}} = \dfrac{1}{{\sqrt 2 }}\end{array}\)
Trong \(\Delta AEB\) , có:
\(cos\varphi = \dfrac{{AE}}{{AB}} = \dfrac{{{U_{R + r}}}}{{75\sqrt 2 }} = \dfrac{1}{{\sqrt 2 }} \Rightarrow {U_{R + r}} = 75V\)
Mà \({U_R} = 35V \Rightarrow {U_r} = 75 - 35 = 40V\)
+ Theo đầu bài ta có, cuộn dây tiêu thụ công suất:
\(\begin{array}{l}P = {I^2}r = I.{U_r} = 40W\\ \Rightarrow I = \dfrac{P}{{{U_r}}} = \dfrac{{40}}{{40}} = 1A\end{array}\)
+ Lại có : \(R + r = \dfrac{{{U_{R + r}}}}{I} = \dfrac{{75}}{1} = 75\Omega \)
Hướng dẫn giải:
Sử dụng giản đồ véc-tơ và hệ thức trong tam giác
Câu hỏi khác
- Đề kiểm tra 1 tiết chương 3: dòng điện xoay chiều - đề số 03 Lý 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 3: dòng điện xoay chiều - đề số 01 Lý 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 3: dòng điện xoay chiều - đề số 02 Lý 12 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 3: dòng điện xoay chiều - đề số 03 Lý 12 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 3: dòng điện xoay chiều - đề số 01 Lý 12 có lời giải chi tiết
