Đặt nguồn âm điểm phát đẳng hướng trong môi trường truyền âm đồng tính không hấp thụ âm. Di chuyển một thiết bị đo mức cường độ âm dọc theo một đường thẳng trong môi trường đó thì thấy mức cường độ âm tại vị trí ban đầu có giá trị \(40 dB\), tăng dần đến giá trị cực đại bằng \(60 dB\) rồi giảm dần và có mức cường độ âm là \(50 dB\) tại vị trí dừng lại. Biết quãng đường di chuyển của thiết bị đo là \(60 m\). Khoảng cách ngắn nhất giữa thiết bị đo với nguồn phát âm gần nhất với giá trị nào sau đây
Trả lời bởi giáo viên
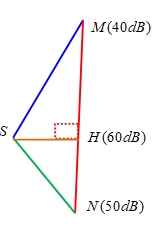
\(\left\{ \begin{array}{l}\underbrace {{L_H} - {L_M}}_{20(dB)} = 20\log \dfrac{{SM}}{{SH}} \to SM = 10SH\\\underbrace {{L_H} - {L_N}}_{10(dB)} = 20\log \dfrac{{SN}}{{SH}} \to SN = \sqrt {10} SH\end{array} \right. \to MH + HN = \underbrace {\sqrt {S{M^2} - S{H^2}} }_{SH\sqrt {99} } + \underbrace {\sqrt {S{N^2} - S{H^2}} }_{SH.3} = 60\)
=> \(SH \approx \)\(4,633(m)\)
Hướng dẫn giải:
Áp dụng công thức tính mức cường độ âm \(L = 10.\log \dfrac{I}{{{I_o}}}\)(dB)

