Câu hỏi:
2 năm trước
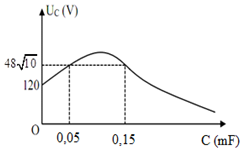
Đặt điện áp \(u = U\sqrt 2 \cos (100t)\;(V)\) vào hai đầu đoạn mạch gồm: điện trở \(R,\) cuộn cảm thuần \(L\) và tụ điện \(C\) mắc nối tiếp. Trong đó \(U, R, L\) không đổi, C có thể thay đổi được. Đồ thị phụ thuộc của \(U_C\) vào \(C\) như hình vẽ. Giá trị của \(L\) là
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có: \({U_C} = \dfrac{{U.{Z_C}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{U}{{\sqrt {\left( {{R^2} + Z_L^2} \right).\dfrac{1}{{Z_C^2}} - 2.{Z_L}.\dfrac{1}{{{Z_C}}} + 1} }}\)
+ Khi \(C = 0 \Rightarrow {Z_C} \to \infty \Rightarrow {U_C} = U = 120V\)
+ Khi \(C = {C_1} = 0,05mF\) và \(C = {C_2} = 0,15mF\) điện áp hiệu dụng hai đầu tụ điện có cùng giá trị:
\(\dfrac{U}{{{Z_1}}}.{Z_{C1}} = \dfrac{U}{{{Z_2}}}.{Z_{C2}} \Rightarrow {U_{C1}} = {U_{C2}} = \dfrac{U}{{\sqrt {1 - \dfrac{{2{Z_L}}}{{{Z_{C1}} + {Z_{C2}}}}} }}\)
\( \Leftrightarrow 48\sqrt {10} = \dfrac{{120}}{{\sqrt {1 - \dfrac{{2L.100}}{{\dfrac{1}{{100.0,{{05.10}^{ - 3}}}} + \dfrac{1}{{100.0,{{15.10}^{ - 3}}}}}}} }} \Rightarrow L = 0,5H\)
Hướng dẫn giải:
Điện áp hiệu dụng hai đầu tụ điện: \({U_C} = \dfrac{U}{Z}.{Z_C} = \dfrac{{U.{Z_C}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Sử dụng kĩ năng đọc đồ thị và biến đổi toán học.
Câu hỏi khác
- Đề thi thử thpt qg sở gdđt hà nội - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg trường thpt chuyên lam sơn - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg sở gdđt kiên giang - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg - đề số 01 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg trường thpt kim liên (2021) Lý 12 có lời giải chi tiết
