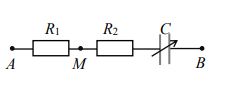
Đặt điện áp \({u_{AB}} = {U_0}\cos \omega t\) (U₀, w không đổi) vào hai đầu đoạn mạch AB như hình bên. Biết \({R_1} = {\rm{ }}3{R_2}\) . Gọi \(\Delta \varphi \) là độ lệch pha giữa \({u_{AB}}\)  và điện áp \({u_{MB}}\). Điều chỉnh điện dung của tụ điện đến giá trị mà \(\Delta \varphi \) đạt cực đại. Hệ số công suất của đoạn mạch AB lúc này bằng:

\({Z_L} = \frac{1}{{\omega L}}\)

\({Z_L} = 2\pi fL\)

\({Z_L} = 2\pi TL\)

\({Z_L} = \frac{{TL}}{{2\pi }}\)

\(R{\rm{ }} = {\rm{ }}{Z_L}-{\rm{ }}{Z_C}\)

\(R{\rm{ }} = {\rm{ }}{Z_L} > {\rm{ }}{Z_{C}}\)

\(R{\rm{ }} = {\rm{ }}{Z_C} - {\rm{ }}{Z_L}\)

\(R{\rm{ }} = {\rm{ }}{Z_C} > {\rm{ }}{Z_L}\)

\({Z_L} = 2{Z_C}\)

\({Z_L} = R\)

\({Z_L} = \frac{{{R^2} + Z_C^2}}{{{Z_C}}}\)

\({Z_L} = {Z_C}\)  

\(\dfrac{{(U_0^2)}}{{4R}}.\)

\(\dfrac{{(U_0^2)}}{{2R}}.\) 

\(U_0^2R\)

\(\dfrac{{U_o^2}}{R}\).

Dòng điện xoay chiều qua điện trở thuần R chỉ có tác dụng nhiệt.

Điện áp ở hai đầu đoạn mạch chỉ có điện trở thuần biến thiên điều hòa cùng tần số, khác pha với cường độ dòng điện.

Cường độ dòng điện qua đoạn mạch chỉ có điện trở thuần biến thiên điều hòa vuông pha với điện áp.

Nhiệt lượng tỏa ra ở điện trở thuần tỉ lệ với cường độ hiệu dụng qua nó.

\(cos\varphi = \dfrac{Z}{{\sqrt {{R^2} + {Z^2}} }}\)                                          

 \(cos\varphi  = \dfrac{Z}{R}\)                          

cosφ = \(\dfrac{R}{{\sqrt {{R^2} + {Z^2}} }}\) 

\(cos\varphi  = \dfrac{R}{Z}\)

\(I = {I_0}\sqrt 2 .\)    

\(I = \dfrac{{{I_0}}}{{\sqrt 2 }}.\)                       

\(I = \dfrac{{{I_0}}}{2}.\)        

\(I = 2{I_0}.\)