Công của trọng lực có giá trị là bao nhiêu khi vật chuyển động được \(5s\)?

Ta có các lực tác dụng lên vật:

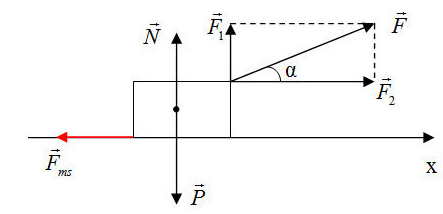
Gắn hệ trục tọa độ như hình vẽ, chọn chiều dương là chiều chuyển động của vật.

Áp dụng định luật II – Niuton ta có: \(\overrightarrow N  + \overrightarrow P  + \overrightarrow {{F_{ms}}}  + \overrightarrow F  = m\overrightarrow a \)  (1)

Chiếu (1) theo các phương, ta có:

Oy: \(N + {F_1} - P = 0 \to N = P - {F_1} = P - F\sin \alpha \)  (2)

Ox: \( - {F_{ms}} + {F_2} = ma \leftrightarrow  - {F_{ms}} + F\cos \alpha  = ma\)     (3)

Lại có: \({F_{ms}} = \mu N = \mu \left( {P - F\sin \alpha } \right)\)

Thay vào (3) ta được:

\(\begin{array}{l} - \mu \left( {P - F\sin \alpha } \right) + Fc{\rm{os}}\alpha  = ma\\ \to a = \dfrac{{F(\mu \sin \alpha  + c{\rm{os}}\alpha ) - \mu .mg}}{m}\\ = \dfrac{{10.\left( {0,2.\sin {{60}^0} + c{\rm{os6}}{{\rm{0}}^0}} \right) - 0,2.2.10}}{2}\\ = 1,366m/{s^2}\end{array}\)

Phương trình quãng đường vật đi được: \(s = \dfrac{1}{2}a{t^2}\) 

=> Quãng đường vật đi được trong \(5s\) là: \(S = \dfrac{1}{2}a{t^2} = \dfrac{1}{2}.1,{366.5^2} = 17,08m\)

Công của lực \(F\) là: \({A_F} = Fs\cos \alpha  = 10.17,08.c{\rm{os6}}{{\rm{0}}^0} = 85,38J\)