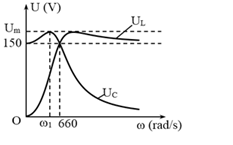
Cho mạch điện xoay chiều gồm một điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp theo thứ tự trên. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có giá trị hiệu dụng không đổi có tần số góc \(\omega \) thay đổi được. Đồ thị biểu diễn sự phụ thuộc vào tần số góc \(\omega \) của điện áp hiệu dụng giữa hai bản tụ và hai đầu cuộn cảm lần lượt là \({U_C},{U_L}\) như hình vẽ dưới. Khi \(\omega  = {\omega _1}\) thì điện áp hiệu dụng giữa hai bản tụ \({U_C}\) cực đại là \({U_m}\). Giá trị của \({U_m}\) là:

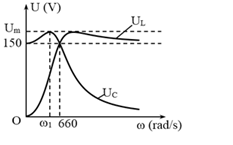
\(\omega  = {\omega _1}\) - thì hiệu điện thế hiệu dụng trên hai đầu tụ điện cực đại  \({U_{{C_{max}}}}\)

+ Từ đồ thị, ta có:

\(\omega  = \omega ' = 0\) và \(\omega  = {\omega _0} = 660\left( {rad/s} \right)\) đều cho \({U_C}\) như nhau

(Áp dụng bài toán \(\omega \) biến thiên có hai giá trị của \(\omega \) cho cùng hiệu điện thế \({U_C}\))

Khi đó ta có:

\(\omega _1^2 + \omega _2^2 = 2\omega _C^2 \Leftrightarrow \omega {'^2} + \omega _0^2 = 2\omega _1^2\)

\( \Rightarrow {\omega _1} = \dfrac{{{\omega _0}}}{{\sqrt 2 }}\)  (1)

+ Tại vị trí \(\omega  = 0\), \({U_C} = U = 150V\)

+ Tại vị trí: \(\omega  = {\omega _0} = 660\left( {rad/s} \right)\), ta có \({U_C} = {U_L} = {U_R} = U\)

Nên ta suy ra: \({Z_{0C}} = {Z_{0L}} = R\)  (2)

+ Tại vị trí: \(\omega  = {\omega _1}\)

\(\begin{array}{l}{U_C} = {U_{{C_{max}}}} = \dfrac{{U{Z_C}}}{Z} = \dfrac{{U{Z_C}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\\ = \dfrac{{U\sqrt 2 {Z_{0C}}}}{{\sqrt {{R^2} + {{\left( {\dfrac{1}{{\sqrt 2 }}{Z_{0L}} - \sqrt 2 {Z_{0C}}} \right)}^2}} }} = \dfrac{{U\sqrt 2 R}}{{\sqrt {{R^2} + {{\left( {\dfrac{1}{{\sqrt 2 }}R - \sqrt 2 R} \right)}^2}} }}\\ = \dfrac{{U\sqrt 2 }}{{\sqrt {1 + \dfrac{1}{2}} }} = \dfrac{{U2\sqrt 3 }}{3}\end{array}\)

Lại có \(U = 150V\)

\( \Rightarrow {U_m} = {U_{{C_{max}}}} = \dfrac{{150.2\sqrt 3 }}{3} = 100\sqrt 3 V\)