Câu hỏi:
2 năm trước
Cho mạch điện như hình vẽ. Trong đó:
\(E = 6V,r = 0,5\Omega ;{R_1} = 1\Omega ;{R_2} = {R_3} = 4\Omega ;{R_4} = 6\Omega \)
Chọn phương án đúng:
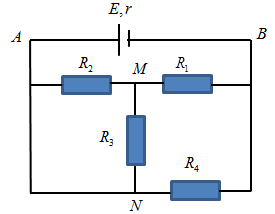
Trả lời bởi giáo viên
Đáp án đúng: a
Vẽ lại mạch điện ta được:
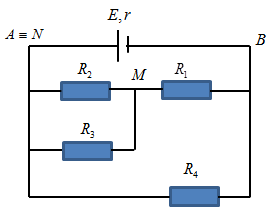
Cấu trúc mạch điện gồm: \(\left[ {\left( {{R_2}//{R_3}} \right)\,\,nt\,{R_1}} \right]//{R_4}\)
Điện trở tương đương của đoạn mạch:
\(\begin{gathered}
\left\{ {\begin{array}{*{20}{l}}
{{R_{23}} = \frac{{{R_2}{R_3}}}{{{R_2} + {R_3}}} = \frac{{4.4}}{{4 + 4}} = 2\Omega } \\
{{R_{123}} = {R_{23}} + {R_1} = 2 + 1 = 3\Omega }
\end{array}} \right. \hfill \\
\Rightarrow {R_{1234}} = \frac{{{R_{123}}.{R_4}}}{{{R_{123}}.{R_4}}} = \frac{{3.6}}{{3 + 6}} = 2\Omega \hfill \\
\end{gathered} \)
Cường độ dòng điện chạy trong mạch chính:
\(I = \dfrac{E}{{{R_{1234}} + r}} = \dfrac{6}{{2 + 0,5}} = 2,4A\)
Công suất của nguồn: \({P_{ng}} = E.I = 6.2,4 = 14,4W\)
Hiệu điện thế giữa hai đầu R4 là:
\({U_4} = {U_{AB}} = E - I.r = 6 - 2,4.0,5 = 4,8V\)
Ta có:
\(\begin{array}{*{20}{l}}
\begin{gathered}
{I_4} = \frac{{{U_4}}}{{{R_4}}} = \frac{{4,8}}{6} = 0,8A \hfill \\
\Rightarrow {I_{23}} = I - {I_4} = 2,4 - 0,8 = 1,6A \hfill \\
\end{gathered} \\
{ \Rightarrow {U_3} = {U_{23}} = {I_{23}}.{R_{23}} = 1,6.2 = 3,2V}
\end{array}\)
Hướng dẫn giải:
Vẽ lại mạch điện
Công thức tính điện trở tương đương của đoạn mạch nối tiếp và song song:
\(\left\{ \begin{array}{l}{R_{nt}} = {R_1} + {R_2}\\\dfrac{1}{{{R_{//}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\end{array} \right.\)
Định luật Ôm đối với toàn mạch: \(I = \dfrac{E}{{{R_N} + r}}\)
Công suất của nguồn: \({P_{ng}} = E.I\)
Câu hỏi khác
- Đề kiểm tra giữa học kì 2 - đề số 1 Lý 11 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 4 Lý 11 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 1 Lý 11 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 05 Lý 11 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 04 Lý 11 có lời giải chi tiết
