Câu hỏi:
2 năm trước
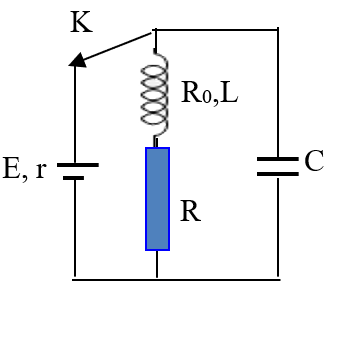
Cho mạch điện như hình vẽ, nguồn có suất điện động E=12V điện trở trong r = 1Ω, tụ có điện dung C=100μF, cuộn dây có hệ số tự cảm L=0,2H và điện trở là R0= 5Ω; điện trở R=18Ω. Ban đầu K đóng, khi trạng thái trong mạch đã ổn định người ta ngắt khoá K. Tính nhiệt lượng tỏa ra trên điện trở R trong thời gian từ khi ngắt K đến khi dao động trong mạch tắt hoàn toàn?
Trả lời bởi giáo viên
Đáp án đúng: c
Khi K đóng \(I_0= \dfrac{E}{(R +r+R_0)} =\dfrac{12}{( 18+1+5)}=0,5A\)
Điện áp 2 đầu tụ C lúc đầu: \(U_0=I_0(R +R_0) = 0,5 .23=11,5V\)
Năng lượng lúc đầu của mạch:
\(\begin{array}{l}W = \dfrac{{CU_0^2}}{2} + \dfrac{{LI_0^2}}{2} = \dfrac{{{{10}^{ - 4}}.11,5_{}^2}}{2} + \dfrac{{0,2.0,5_{}^2}}{2}\\ = {0,66125.10^{ - 2}} + 0,025 = 0,0316125J\end{array}\)
Năng lượng tỏa ra trên R và R0 tỉ lệ thuận với điện trở.
\(\to \dfrac{R}{R_0}=\dfrac{18}{5}\)
\(\to\) Nhiệt lượng tỏa ra chia thành 23 phần thì tỏa trên R 18 phần.
Khi mạch tắt hoàn toàn thì năng lượng W chuyển thành nhiệt lượng tỏa ra trên
R và R0 nên ta có: \(Q=W\)
\(\to\) Nhiệt lượng tỏa ra trên R: \(Q_R = \dfrac{{18}}{{23}}W = \dfrac{{18}}{{23}}.0,0316125 = 0,024740217J \approx 0,02474J=24,74 mJ\).
Hướng dẫn giải:
- Sử dụng định luật ohm: I = E /(R + r)
- Năng lượng của mạch dao động: \(W = \dfrac{1}{2}L{i^2} + \dfrac{1}{2}C{u^2}\)
