Cho hình bình hành $ABCD$ có \(\widehat A = \alpha  > 90^\circ \) . Ở phía ngoài hình bình hành vẽ các tam giác đều $ADE,ABF$. Tam giác \(CEF\) là tam giác gì?  Chọn câu trả lời đúng nhất

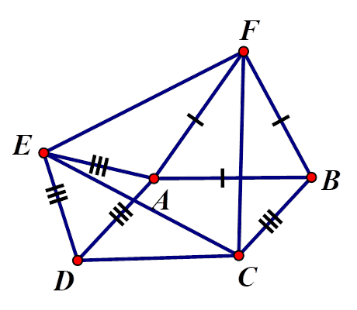
 Ta có:

\(\widehat {EAF} = 360^\circ  - \widehat {BAF} - \widehat {EAD} - \alpha \) \( = 360^\circ  - 60^\circ  - 60^\circ  - \alpha  = 240^\circ  - \alpha \)

Ta có:\(\widehat {ADC} = 180^\circ  - \alpha \) ; \(\widehat {CDE} = \widehat {ADC} + \widehat {EDA} = 180^\circ  - \alpha  + 60^\circ  = 240^\circ  - \alpha \)\( \Rightarrow \widehat {CDE} = \widehat {FAE}\)

Xét \(\Delta CDE\) và \(\Delta FAE\) có:

\(\left\{ \begin{array}{l}CD = FA(gt)\\\widehat {CDF} = \widehat {EAF}(cmt)\\DE = EA(gt)\end{array} \right.\)\( \Rightarrow \Delta CDE = \Delta FAE\left( {c.g.c} \right) \Rightarrow CE = FE\,\,(1)\)

Tương tự , ta có:

\(\widehat {ABC} = 180^\circ  - \alpha \) ; \(\widehat {CBF} = \widehat {ABC} + \widehat {FBA} = 180^\circ  - \alpha  + 60^\circ  = 240^\circ  - \alpha  \Rightarrow \widehat {CBF} = \widehat {FAE}\)

Xét \(\Delta FBC\) và \(\Delta FAE\) có:

\(\left\{ \begin{array}{l}FB = FA(gt)\\\widehat {CBF} = \widehat {EAF}(cmt)\\CB = EA(gt)\end{array} \right.\)\( \Rightarrow \Delta FBC = \Delta FAE\left( {c.g.c} \right) \Rightarrow CF = FE\,\,(2)\)

Từ (1) và (2) suy ra \(CF = FE = EC\) nên tam giác $CEF$ đều.