Câu hỏi:
2 năm trước
Cho hệ vật như hình vẽ:
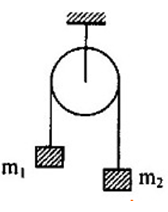
Biết \({m_1} = 2{m_2}\). Lực căng của dây treo ròng rọc là \(52,3N\). Khối lượng của \({m_2}\) có giá trị là:
Trả lời bởi giáo viên
Đáp án đúng: a
- Vì bỏ qua khối lượng ròng rọc nên ta có: \(T' = 2T \to T = \frac{{T'}}{2} = \frac{{52,3}}{2} = 26,15N\)
\({m_1} > {m_2} \to {m_1}\) đi xuống, \({m_2}\) đi lên.
- Chọn chiều dương là chiều chuyển động của hệ
- Các lực tác dụng lên hệ gồm: các trọng lực \(\overrightarrow {{P_1}} ;\overrightarrow {{P_2}} \)
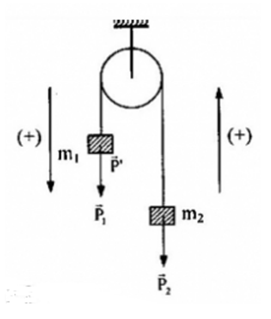
- Viết phương trình định luật II - Niutơn, ta được:
\(\overrightarrow {{P_1}} + \overrightarrow {{P_2}} = \left( {{m_1} + {m_2}} \right)\overrightarrow a {\rm{ }}\left( 1 \right)\)
- Chiếu (1) lên chiều dương, ta được:
\(\begin{array}{l}{P_1} - {P_2} = \left( {{m_1} + {m_2}} \right)a \leftrightarrow {m_1}g - {m_2}g = \left( {{m_1} + {m_2}} \right)a\\ \to a = \frac{{{m_1} - {m_2}}}{{{m_1} + {m_2}}}g = \frac{{2{m_2} - {m_2}}}{{2{m_2} + {m_2}}}g = \frac{1}{3}.9,8 = 3,27m/{s^2}\end{array}\)
Xét riêng vật \({m_2}\), ta có:
\(\begin{array}{l}T - {P_2} = {m_2}a \to T - {m_2}g = {m_2}a\\ \to {m_2} = \frac{T}{{g + a}} = \frac{{26,15}}{{9,8 + 3,27}} = 2kg\end{array}\)
Hướng dẫn giải:
+ Xác định lực căng T
+ Chọn chiều dương
+ Xác định các lực tác dụng lên hệ
+ Viết phương trình định luật II - Niutơn cho hệ
+ Chiếu phương trình ĐL II - Niutơn của hệ
+ Xét riêng phương trình ĐL II của vật \({m_2}\)
Câu hỏi khác
- Đề kiểm tra 1 tiết chương 2: động lực học chất điểm - đề số 04 Lý 10 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 2: động lực học chất điểm - đề số 02 Lý 10 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 2: động lực học chất điểm - đề số 02 Lý 10 có lời giải chi tiết
- Đề kiểm tra 1 tiết chương 2: động lực học chất điểm - đề số 03 Lý 10 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 2: động lực học chất điểm - đề số 03 Lý 10 có lời giải chi tiết
