Cho đoạn mạch nối tiếp gồm các phần tử như hình vẽ trong đó R = r = 50 Ω. Đặt điện áp xoay chiều có biểu thức u = U0cos(ωt) vào hai đầu đoạn mạch. Đồ thị biểu diễn điện áp ở hai đầu đoạn mạch AN và MB biểu diễn như hình vẽ. Dung kháng của tụ điện bằng
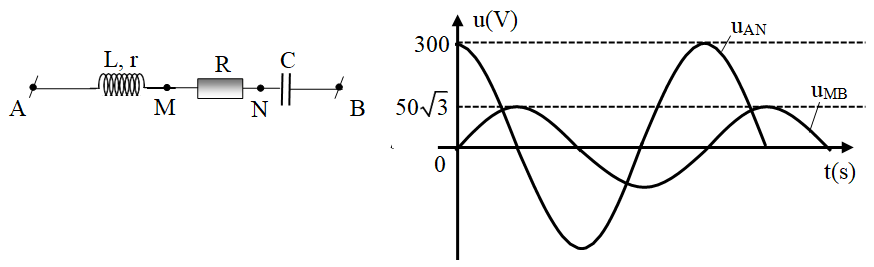
Trả lời bởi giáo viên
Từ đồ thị ta thấy pha ban đầu của điện áp uAN và uMB là:
\(\left\{ \begin{array}{l}{\varphi _{AN}} = {\varphi _1} = 0\\{\varphi _{MB}} = {\varphi _2} = - \dfrac{\pi }{2}\end{array} \right. \Rightarrow \overrightarrow {{U_{AN}}} \bot \overrightarrow {{U_{MB}}} \)
Ta có: \(\tan {\varphi _1}.\tan {\varphi _2} = - 1\)
\( \Rightarrow \dfrac{{{Z_L}}}{{R + r}}.\dfrac{{ - {Z_C}}}{R} = - 1 \Rightarrow {Z_L} = \dfrac{{R.\left( {R + r} \right)}}{{{Z_C}}} = \dfrac{{5000}}{{{Z_C}}}\)
Lại có: \(\dfrac{{{U_{0AN}}}}{{{U_{0MB}}}} = \dfrac{{{Z_{AN}}}}{{{Z_{MB}}}}\)
\(\begin{array}{l} \Rightarrow \dfrac{{300}}{{50\sqrt 3 }} = \dfrac{{\sqrt {{{\left( {R + r} \right)}^2} + {Z_L}^2} }}{{\sqrt {{R^2} + {Z_C}^2} }} = \dfrac{{\sqrt {{{100}^2} + {Z_L}^2} }}{{\sqrt {{{50}^2} + {Z_C}^2} }}\\ \Rightarrow \dfrac{{{{100}^2} + {Z_L}^2}}{{{{50}^2} + {Z_C}^2}} = \dfrac{{{{300}^2}}}{{{{\left( {50\sqrt 3 } \right)}^2}}} = 12\\ \Rightarrow 12{Z_C}^2 - {Z_L}^2 + 20000 = 0\\ \Rightarrow 12{Z_C}^2 - \dfrac{{{{5000}^2}}}{{{Z_C}^2}} + 20000 = 0\\ \Rightarrow {Z_C}^2 = \dfrac{{2500}}{3} \Rightarrow {Z_C} = \dfrac{{50}}{{\sqrt 3 }} = \dfrac{{50\sqrt 3 }}{3}\,\,\left( \Omega \right)\end{array}\)
Hướng dẫn giải:
Sử dụng kĩ năng đọc đồ thị
Độ lệch pha giữa điện áp và cường độ dòng điện: \(\tan \varphi = \dfrac{{\left| {{Z_L} - {Z_C}} \right|}}{{R + r}}\)
Hai điện áp vuông pha có: \(\tan {\varphi _1}.\tan {\varphi _2} = - 1\)
Cường độ dòng điện trong mạch: \({I_0} = \dfrac{{{U_{0AN}}}}{{{Z_{AN}}}} = \dfrac{{{U_{0MB}}}}{{{Z_{MB}}}}\)

