Câu hỏi:
2 năm trước
Cho đoạn mạch AB theo thứ tự gồm cuộn dây thuần cảm có độ tự cảm \(L\), một đoạn mạch \(X\) và tụ điện có điện dung \(C\) mắc nối tiếp. Gọi \(M\) là điểm nối giữa \(L\) và \(X\), \(N\) là điểm nối giữa \(X\) và \(C\). Đặt vào hai đầu đoạn mạch xoay chiều \(u = {U_0}\cos \omega t\), với ω thỏa mãn điều kiện \(LC{\omega ^2} = 1\). Khi đó điện áp hiệu dụng của đoạn mạch \(AN\) (chứa \(L\) và \(X\)) gấp \(\sqrt 3 \) lần điện áp hiệu dụng của đoạn mạch \(MB\) (chứa \(X\) và \(C\)). Độ lệch pha lớn nhất giữa điện áp của cuộn dây và đoạn mạch \(X\) bằng
Trả lời bởi giáo viên
Đáp án đúng: d
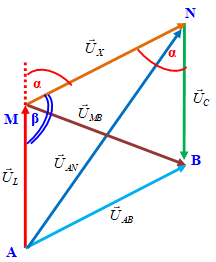
+ \(U_{AN}^2 = 3U_{MB}^2 \to U_L^2 + U_X^2\underbrace { - 2{U_L}{U_X}{\rm{cos}}\beta }_{ - c{\rm{os}}\beta = c{\rm{os}}\alpha } = 3(\underbrace {U_C^2}_{U_L^2} + U_X^2 - 2\underbrace {{U_C}}_{{U_L}}{U_X}{\rm{cos}}\alpha {\rm{)}}\)
=> \(4{U_L}{U_X}{\rm{cos}}\alpha = U_L^2 + U_X^2 \ge 2{U_L}.{U_X}\) (Theo cosi)
=> \({\rm{cos}}\alpha \ge \dfrac{1}{2} \to \)\(\alpha \le \dfrac{\pi }{3}\)
Hướng dẫn giải:
+ Sử dụng giản đồ vecto
+ Sử dụng định lý hàm số cos:\({c^2} = {a^2} + {b^2} - 2ab.cos\varphi \)
+ Sử dụng bất đẳng thức cosi: a+b\( \ge \)2ab
+ Khi \(LC{\omega ^2} = 1\), xảy ra hiện tượng cộng hưởng, \({U_L} = {U_C}\)
Câu hỏi khác
- Đề thi thử thpt qg sở gdđt hà nội - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg trường thpt chuyên lam sơn - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg sở gdđt kiên giang - 2021 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg - đề số 01 Lý 12 có lời giải chi tiết
- Đề thi thử thpt qg trường thpt kim liên (2021) Lý 12 có lời giải chi tiết
