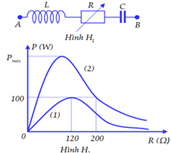
Cho đoạn mạch \(AB\) như hình \(H_1\) với \(L\) là cuộn cảm thuần, \(R\) là biến trở. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có biểu thức \(u =\) \(U\sqrt 2 cos2\pi ft\)(V), \(U\) không đổi nhưng \(f\) có thể thay đổi được. Hình \(H_2\) là đồ thị biểu diễn sự phụ thuộc của công suất tiêu thụ điện của mạch theo \(R\) là đường \((1)\) khi \(f = f_1\) và là đường \((2)\) khi \(f = f_2\). Bỏ qua điện trở của dây nối. Giá trị của \(P_{max}\) gần nhất với giá trị nào sau đây ?   

Trong chân không, các bức xạ có bước sóng trong khoảng từ \(3.10^{-9}m\) đến \(3.10^{-7}m\) là

Một sóng âm truyền qua điểm \(M\) với cường độ âm là \(I\). Biết cường độ âm chuẩn là \(I_0\). Mức cường độ âm \(L\) (\(dB\)) của sóng âm này tại \(M\) được tính bằng công thức

Một mạch dao động LC lí tưởng đang có dao động điện từ tự do. Cường độ dòng điện trong mạch có biểu thức là \(I = {2.10^{ - 2}}\cos ({2.10^6}t)(A)\) , \(t\) tính bằng giây. Điện tích cực đại của tụ điện là

Trong không khí, phôtôn \(A\) có bước sóng lớn gấp \(n\) lần bước sóng của phôtôn \(B\) thì tỉ số giữa năng lượng phôtôn \(A\) và năng lượng phôtôn \(B\) là:

Tia nào sau đây không phải là tia phóng xạ?  

Chiếu một ánh sáng có bước sóng \(λ\) và năng lượng phôtôn là \(ɛ\) vào một chất huỳnh quang thì ánh sáng phát quang có bước sóng \(λ’\) và năng lượng phôtôn là \(ɛ’\). Biết

\(\dfrac{{\varepsilon '}}{\varepsilon } = 0,8\). Tỉ số \(\dfrac{{\lambda '}}{\lambda }\) bằng

Hợp lực tác dụng lên vật dao động điều hòa: