Cần tác dụng lên vật m trên mặt phẳng nghiêng góc \(\alpha \) một lực F bằng bao nhiêu để vật nằm yên, hệ số ma sát giữa vật và mặt phẳng nghiêng là \(\mu \) , khi biết vật có xu hướng trượt xuống.

Phân tích các lực tác dụng ta có hình vẽ:

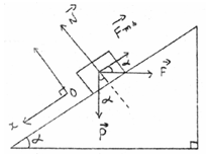
Chọn hệ trục Oxy như hình vẽ

Áp dụng định luật II Newton ta có: \(\overrightarrow F  + \overrightarrow P  + \overrightarrow N  + \overrightarrow {{F_{m{\rm{s}}}}}  = 0\)(1)

(a = 0 khi vật đứng yên trên mặt phẳng nghiêng )

Chiếu (1) lên Oy ta được: \(N - Pco{\rm{s}}\alpha {\rm{ - F}}\sin \alpha  = 0\)

\( \Rightarrow N = Pco{\rm{s}}\alpha {\rm{ + F}}\sin \alpha \)

ta có: \({F_{m{\rm{s}}}} = \mu N \Rightarrow {F_{m{\rm{s}}}} = \mu \left( {Pco{\rm{s}}\alpha {\rm{ + F}}\sin \alpha } \right) = \mu \left( {mgco{\rm{s}}\alpha {\rm{ + F}}\sin \alpha } \right)\)

Chiếu (1) lên Ox ta được: \(P\sin \alpha  - Fco{\rm{s}}\alpha  - {{\rm{F}}_{m{\rm{s}}}} = 0\)

\(\begin{array}{l} \Rightarrow Fco{\rm{s}}\alpha  = P\sin \alpha  - {F_{m{\rm{s}}}}\\ \Rightarrow Fco{\rm{s}}\alpha  = mg\sin \alpha  - \mu mgco{\rm{s}}\alpha {\rm{ - }}\mu {\rm{F}}\sin \alpha \\ \Rightarrow F = \dfrac{{mg\left( {\sin \alpha  - \mu co{\rm{s}}\alpha } \right)}}{{co{\rm{s}}\alpha {\rm{ + }}\mu {\rm{sin}}\alpha }}\\ \Rightarrow F = \dfrac{{mg\left( {tg\alpha  - \mu } \right)}}{{1 + \mu .tg\alpha }}\end{array}\)