Câu hỏi tr 106
| Mở đầu: Các đối tượng chuyển động tròn được gặp khá thường xuyên, ở mọi mức độ. Các bánh xe, bánh răng ròng rọc, vận động viên đua mô tô khi vào khúc quanh hay vệ tinh của Trái Đất – tất cả đều tham gia chuyển động tròn. Cái gì làm một vật chuyển động tròn? Sự hiểu biết về chuyển động tròn giữ vai trò quan trọng như thế nào trong cuộc sống, khoa học và kĩ thuật?
|
Phương pháp giải:
Vận dụng kiến thức đã học để áp dụng vào thực tế
Lời giải chi tiết:
Lực làm vật chuyển động tròn là lực hướng tâm
Sự hiểu biết về chuyển động tròn giữ vai trò quan trọng trong cuộc sống, khoa học và kĩ thuật:
+ Nhờ chuyển động tròn mà con người đã chế tạo ra chiếc đồng hồ, bánh xe, giải thích được một số hiện tượng thiên văn,...
Quan sát, trả lời câu hỏi và thảo luận
| Lấy các ví dụ trong thực tế và thảo luận xem chuyển động nào là chuyển động tròn. |
Phương pháp giải:
Liên hệ thực tế:
Lời giải chi tiết:
Ví dụ:
+ Đồng hồ: chuyển động tròn của kim giờ, kim phút, kim giây là chuyển động tròn
+ Chuyển động tròn của bánh xe máy, xe đạp, xe ô tô
Câu hỏi tr 107
Luyện tập
| Câu 1: Đổi các góc sau từ độ sang radian: 300 , 900 , 1050 , 1200 , 2700 . |
Phương pháp giải:
\(\begin{array}{l}1radian = \frac{{{{360}^0}}}{{2\pi }} = \frac{{{{180}^0}}}{\pi }\\{1^0} = \frac{\pi }{{180}}rad\end{array}\)
Lời giải chi tiết:
\(\begin{array}{l}{30^0} = \frac{{30.\pi }}{{180}}rad = \frac{\pi }{6}rad\\{90^0} = \frac{{90.\pi }}{{180}}rad = \frac{\pi }{2}rad\\{105^0} = \frac{{105.\pi }}{{180}}rad = \frac{{7\pi }}{{12}}rad\\{120^0} = \frac{{120.\pi }}{{180}}rad = \frac{{2.\pi }}{3}rad\\{270^0} = \frac{{270.\pi }}{{180}}rad = \frac{{3.\pi }}{2}rad\end{array}\)
| Câu 2: Đổi các góc sau từ radian sang độ: 0,5 rad; 0,75 rad; π rad. |
Phương pháp giải:
\(\begin{array}{l}1radian = \frac{{{{360}^0}}}{{2\pi }} = \frac{{{{180}^0}}}{\pi }\\{1^0} = \frac{\pi }{{180}}rad\end{array}\)
Lời giải chi tiết:
\(\begin{array}{l}0,5rad = 0,5.\frac{{{{180}^0}}}{\pi } \approx 28,{6^0}\\0,75rad = 0,75.\frac{{{{180}^0}}}{\pi } \approx {43^0}\\\pi rad = \pi .\frac{{{{180}^0}}}{\pi } = {180^0}\end{array}\)
Câu hỏi tr 108
Luyện tập
| Câu 1: So sánh tốc độ chuyển động của đầu kim giây, đầu kim phút và đầu kim giờ? |
Phương pháp giải:
Liên hệ thực tế và vận dụng khả năng quan sát, suy luận
Lời giải chi tiết:
Ta thấy để đi hết 1 vòng tròn, kim giây mất 60 s, kim phút mất 60 phút = 3600 s, kim giờ mất 12 h = 43200 s
=> Kim giây có tốc độ chuyển động nhanh nhất và kim giờ có tốc độ chuyển động chậm nhất.
| Câu 2: Một đồng hồ điểm 3h30ph. Hãy tính góc quay từ vị trí 12h đến vị trí của kim phút và kim giờ. |
Phương pháp giải:
Liên hệ thực tế và vận dụng khả năng quan sát, suy luận
Lời giải chi tiết:


Kim phút:
+ Tại 12 h kim phút chỉ số 12, đến 3h30ph thì kim phút chỉ số 6, ta thấy kim phút đi được một nửa vòng tròn
+ 1 vòng tròn = 3600 => 1 nửa vòng tròn = 1800
Kim giờ
+ 1 giờ, kim giờ quay được 1 góc là 300
=> Từ 12h đến 3h30ph tương ứng là 3,5 h thì kim giờ quay được 1 góc là 3,5.30 = 1050
| Câu 3: Tính tốc độ góc của kim giờ và kim phút của đồng hồ. |
Phương pháp giải:
Mối liên hệ giữa chu kì, tốc độ góc: \(\omega = \frac{{2\pi }}{T}\)
Lời giải chi tiết:
Chu kì của kim giờ là 43200 s
=> Tốc độ góc của kim giờ là \(\omega = \frac{{2\pi }}{T} = \frac{{2.\pi }}{{43200}} \approx 1,{45.10^{ - 4}}(rad/s)\)
Chu kì của kim phút là 3600 s
=> Tốc độ góc của kim giây là \(\omega = \frac{{2\pi }}{T} = \frac{{2.\pi }}{{3600}} \approx 1,{75.10^{ - 3}}(rad/s)\)
Quan sát, trả lời câu hỏi và thảo luận
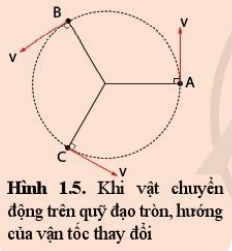
| Giải thích vì sao toàn bộ các mũi tên trên hình 1.5 đều được vẽ với độ dài như nhau
|
Lời giải chi tiết:
Do vật chuyển động tròn đều nên tốc độ không thay đổi, hay vật dịch chuyển được các cung tròn có số đo góc bằng nhau sau những khoảng thời gian bằng nhau.
Luyện tập
| Một em bé cưỡi ngựa gỗ trên sàn quay, ở cách trục quay 2,1 m. Tốc độ góc của sàn quay là 0,42 rad/s. Tính tốc độ của ngựa gỗ. |
Phương pháp giải:
Mối liên hệ giữa tốc độ, tốc độ góc và bán kính: \(v = \omega .r\)
Trong đó:
+ \(\omega \)là tốc độ góc (rad/s)
+ v là tốc độ (m/s)
+ r là bán kính (m)
Lời giải chi tiết:
Ta có: \(\omega \)= 0,42 rad/s; r = 2,1 m.
Tốc độ của ngựa gỗ là: \(v = \omega .r = 0,42.2,1 = 0,882(m/s)\)
Câu hỏi tr 109
Quan sát, trả lời câu hỏi và thảo luận
| Dựa vào đơn vị SI của các đại lượng, hãy chứng tỏ tính đúng đắn của biểu thức (4) |
Phương pháp giải:
7 đơn vị cơ bản trong hệ SI:
+ Quãng đường: m
+ Thời gian: s
+ Nhiệt độ: K
+ Khối lượng: kg
+ Cường độ dòng điện: A
+ Khối lượng chất: mol
+ Cường độ sáng: Cd
Lời giải chi tiết:
Biểu thức (4): \(v = \omega .r\)
Ta biểu diễn biểu thức (4) sang đơn vị, ta có:
\(\left[ {\frac{m}{s}} \right] = \left[ {\frac{1}{s}} \right].\left[ m \right]\)
=> Biểu thức (4) đúng
Quan sát, trả lời câu hỏi và thảo luận
| Lực gây ra gia tốc của chuyển động tròn đều có hướng như thế nào? |
Lời giải chi tiết:
Lực gây ra gia tốc của chuyển động tròn đều có hướng vào tâm quỹ đạo tròn và có tên là lực hướng tâm.
Câu hỏi tr 110
Luyện tập
| Hai điểm A và B nằm trên cùng một bán kính của một vô lăng đang quay đều, cách nhau 20 cm. Điểm A ở phía ngoài tốc độ 0,6 m/s, điểm B ở phía trong (gần trục quay hơn) có tốc độ 0,2 m/s. Tính tốc độ góc của vô lăng. |
Phương pháp giải:
Mối liên hệ giữa tốc độ, tốc độ góc và bán kính: \(v = \omega .r\)
Lời giải chi tiết:
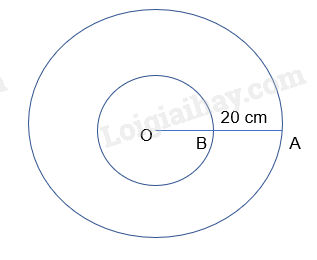
Trong chuyển động tròn đều, tốc độ góc có giá trị không thay đổi
=> \(\omega = \frac{{{v_A}}}{{{r_A}}} = \frac{{{v_B}}}{{{r_B}}}\)
\( \Rightarrow \frac{{{r_A}}}{{{r_B}}} = \frac{{{v_A}}}{{{v_B}}} = \frac{{0,6}}{{0,2}} = 3\) (1)
Mặt khác, ta có AB = 20 cm = 0,2 m
=> \({r_A} - {r_B} = 0,2\) (2)
Từ (1) và (2) => rA = 0,3 m; rB = 0,1 m.
Tốc độ góc của vô lăng là: \(\omega = \frac{{{v_A}}}{{{r_A}}} = \frac{{0,6}}{{0,3}} = 2(rad/s)\)
Luyện tập
| Áp dụng định luật II Newton, hãy rút ra biểu thức tính độ lớn của lực hướng tâm |
Phương pháp giải:
Biểu thức định luật II Newton: F = m.a
Biểu thức gia tốc hướng tâm: \({a_{ht}} = \frac{{{v^2}}}{r}\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}{F_{ht}} = m.{a_{ht}} = m.\frac{{{v^2}}}{r} = m.r.{\left( {\frac{v}{r}} \right)^2} = m.r.{\omega ^2}\\ \Rightarrow {F_{ht}} = \frac{{m{v^2}}}{r} = mr{\omega ^2}\end{array}\)
Vận dụng
| Trạm không gian quốc tế ISS có tổng khối lượng 350 tấn, quay quanh Trái Đất ở độ cao 340 km, nơi có gia tốc trọng trường 8,8 m/s2 . Bán kính Trái Đất là 6400 km. Tính: a) Lực hướng tâm tác dụng lên Trạm không gian. b) Tốc độ của Trạm không gian trên quỹ đạo. c) Thời gian quay quanh Trái Đất của Trạm không gian. d) Số vòng Trạm không gian thực hiện quanh Trái Đất trong một ngày. |
Phương pháp giải:
- Biểu thức tính lực hướng tâm: F = m.a
- Mối liên hệ giữa a,v,R: \(a = \frac{{{v^2}}}{R} = \frac{{{v^2}}}{{r + h}}\)
Trong đó r là khoảng cách từ mặt đất đến tâm Trái Đất, h là độ cao của vật so với mặt đất (nếu vật tại mặt đất thì h = 0)
Biểu thức tính chu kì: \(T = \frac{{2.\pi .R}}{v}\)
Lời giải chi tiết:
a) Lực hướng tâm tác dụng lên Trạm không gian là trọng lực của Trạm
=> Fht = P = m.g = 350.103 .8,8 = 3,08.106 (N)
b) Tốc độ của Trạm không gian là:
\(g = \frac{{{v^2}}}{{r + h}} \Rightarrow v = \sqrt {g(r + h)} = \sqrt {8,8.(6400 + 340){{.10}^3}} \approx 7701,43(m/s)\)
c) Thời gian quay quanh Trái Đất của Trạm không gian
\(T = \frac{{2.\pi .(r + h)}}{v} = \frac{{2.\pi .(6400 + 340){{.10}^3}}}{{7701,43}} \approx 5499(s)\)
d) Đổi 1 ngày = 86400 s
Số vòng Trạm không gian thực hiện quanh Trái Đất trong một ngày
\(n = \frac{t}{T} = \frac{{86400}}{{5499}} \approx 16\)(vòng).
Quan sát, trả lời câu hỏi và thảo luận
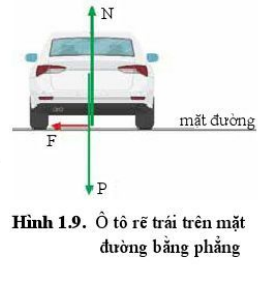
| Trong hình 1.9, ô tô muốn rẽ với khúc cua rộng hơn và với tốc độ lớn hơn. Làm thế nào để người lái xe rẽ trái an toàn?
|
Phương pháp giải:
Vận dụng kiến thức đã học
Lời giải chi tiết:
Ô tô đang đi theo hướng vuông góc với tờ giấy, trên một mặt đường bằng phẳng và rẽ trái. Đường tác dụng lên ô tô 2 lực. Lực thứ nhất là phản lực vuông góc với mặt đường, lực này cân bằng với trọng lực của ô tô. Vì vậy ô tô không có gia tốc theo phương thẳng đứng. Lực thứ hai là lực ma sát nghỉ của bánh xe với mặt đường. Lực ma sát nghỉ không cân bằng với lực nào và đóng vai trò là lực hướng tâm. Lực ma sát cần có độ lớn thỏa mãn \(F = \frac{{m{v^2}}}{r}\) để có thể rẽ trái an toàn với tốc v theo quỹ đạo có bán kính r mong muốn
Câu hỏi tr 111
Tìm hiểu thêm
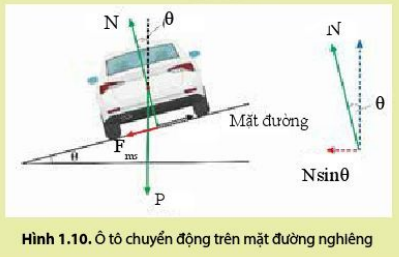
| Khi chiếc ô tô chuyển động trên mặt đường nghiêng với góc nghiêng nhỏ (hình 1.10), thì các thành phần theo phương thẳng đứng của phản lực N và của lực ma sát cân bằng với trọng lực P = m.g của xe, còn các thành phần theo phương nằm ngang của phản lực N và của lực ma sát đóng vai trò lực hướng tâm. Do đó, theo phương ngang \(N\sin \theta + {F_{ms}}\cos \theta = \frac{{m{v^2}}}{r}\) Với r là bán kính cung đường, v là tốc độ của xe. Thảo luận về các yếu tố ảnh hưởng của góc nghiêng của mặt đường tới sự an toàn của xe khi vào khúc đường quanh tròn.
|
Lời giải chi tiết:
Từ biểu thức \(N\sin \theta + {F_{ms}}\cos \theta = \frac{{m{v^2}}}{r}\), ta có các yếu tố ảnh hưởng đến góc nghiêng của mặt đường tới sự an toàn của xe khi vào khúc đường quanh tròn:
+ Lực ma sát của bánh xe với mặt đường, nếu lực ma sát không đủ lớn thì xe có thể bị văng ra khỏi khúc cua
+ Tốc độ của xe
+ Bán kính của cung đường
Câu hỏi tr 112
Vận dụng: Trong mỗi tình huống trong hình 1.11, lực nào đóng vai trò là lực hướng tâm? Thảo luận về các điều kiện đảm bảo an toàn của chuyển động trong mỗi tình huống.
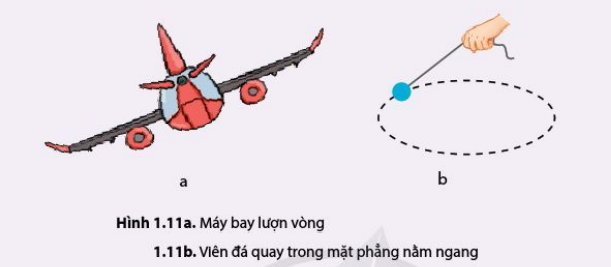
| Câu 1: Chiếc máy bay đang lượn vòng. Để chuyển hướng, người phi công làm nghiêng cánh máy bay (hình 1.11a). |
Phương pháp giải:
Phân tích lực
Lời giải chi tiết:
Lực đóng vai trò lực hướng tâm là trọng lực
Điều kiện để đảm bảo an toàn cho chuyển động của máy bay:
+ Tốc độ chuyển động của máy bay
+ Góc nghiêng giữa cánh máy bay với mặt phẳng ngang.
| Câu 2: Một viên đá được buộc vào một sợi dây và quay tròn trong mặt phẳng ngang tạo thành hình nón (hình 1.11b) |
Phương pháp giải:
Phân tích lực
Lời giải chi tiết:
Lực đóng vai trò lực hướng tâm là lực căng của sợi dây buộc với vật
Điều kiện để đảm bảo an toàn cho chuyển động của viên đá
+ Tốc độ chuyển động của viên đá
+ Góc nghiêng của dây so với phương thẳng đứng
+ Lực quay của tay