Vết của các hạt \({\beta ^ - }\) và \({\beta ^ + }\) phát ra từ nguồn N chuyển động trong từ trường \(\vec B\) có dạng như hình vẽ. So sánh động năng của hai hạt này ta thấy
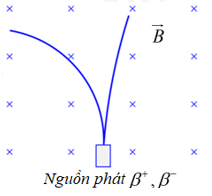
Trả lời bởi giáo viên
Áp dụng quy tắc bàn tay trái ta xác định được nguồn phát và chiều của lực từ tác dụng như sau:
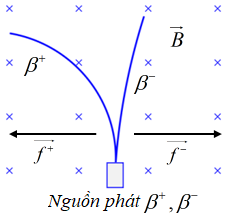
Lực tác dụng lên điện tích chuyển động trong từ trường:
\(f = qvB.\sin \alpha = qvB.\sin 90 = qvB \Rightarrow f \sim v\)
Lại có: \(\left\{ \begin{array}{l}{W_{d + }} = \dfrac{1}{2}{m_{\beta + }}.v_{\beta + }^2\\{W_{d - }} = \dfrac{1}{2}{m_{\beta - }}.v_{\beta - }^2\\{m_{\beta + }} = {m_{\beta - }}\end{array} \right.\)
Từ hình vẽ ta thấy tia \({\beta ^ + }\) lệch nhiều hơn tia \({\beta ^ - }\) nên \({f^ + } > {f^ - }\)
\( \Rightarrow {v^ + } > {v^ - } \Rightarrow {W_{d + }} > {W_{d - }}\)
Vậy động năng của hạt \({\beta ^ - }\)nhỏ hơn.
Hướng dẫn giải:
+ Lực Lo-ren-xơ tác dụng lên một hạt điện tích \({q_0}\) chuyển động trong một từ trường \(\vec B\) có phương vuông góc với \(\vec v\) và \(\vec B\), có chiều tuân theo quy tắc bàn tay trái và có độ lớn: \(f = \left| {{q_0}} \right|vB.\sin \alpha \)
Trong đó \(\alpha = \left( {\vec v;\vec B} \right)\)
+ Quy tắc bàn tay trái: “Để bàn tay trái mở rộng sao cho từ trường hướng vào lòng bàn tay, chiều từ cổ tay đến ngón giữa là chiều của \(\overrightarrow v \) khi \({q_0} > 0\) và ngược chiều \(\overrightarrow v \) khi \({q_0} < 0\). Lúc đó chiều của lực Lo-ren-xơ là chiều ngón cái choãi ra.
+ Sử dụng lí thuyết về tia \(\beta \): Loại phổ biến là \({\beta ^ - }\). Đó chính là các electron. Loại hiếm hơn là tia \({\beta ^ + }\). Đó chính là các pozitron, hay electron dương, có cùng khối lượng với như electron, nhưng mang điện tích nguyên tố dương.
+ Công thức tính động năng: \({W_d} = \frac{1}{2}m{v^2}\)
Câu hỏi khác
- Đề thi môn khoa học tự nhiên, công nghệ và khoa học xã hội - đề số 1 Khoa học tự nhiên, công nghệ và khoa học xã hội Đánh giá năng lực Đại học Quốc gia Hà Nội có lời giải chi tiết
- Đề thi môn khoa học tự nhiên, công nghệ và khoa học xã hội - đề số 2 Khoa học tự nhiên, công nghệ và khoa học xã hội Đánh giá năng lực Đại học Quốc gia Hà Nội có lời giải chi tiết
- Đề thi môn khoa học tự nhiên, công nghệ và khoa học xã hội - đề số 6 Đánh giá năng lực Đại học Quốc gia Hà Nộicó lời giải chi tiết
- Đề thi môn khoa học tự nhiên, công nghệ và khoa học xã hội - đề số 3 Đánh giá năng lực Đại học Quốc gia Hà Nội có lời giải chi tiết
- Đề thi môn khoa học tự nhiên, công nghệ và khoa học xã hội - đề số 5 Khoa học tự nhiên, công nghệ và khoa học xã hội Đánh giá năng lực Đại học Quốc gia Hà Nội có lời giải chi tiết
