Thực hiện thí nghiệm Y-âng về giao thoa ánh sáng, nguồn sáng điểm S phát ra ánh sáng đơn sắc có bước sóng 500 nm. Khoảng cách giữa hai khe S1 và S2 là 1 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 2 m. Ban đầu, S đặt tại điểm O nằm trên đường trung trực của S1S2 và cách mặt phẳng chứa hai khe 50 cm. Xét trục Ou song song với màn và vuông góc với mặt phẳng trung trực của hai khe S1S2 như hình vẽ, trong đó 0 là gốc tọa độ. Giữ nguyên các điều kiện khác, cho S dao động điều hòa trên trục Ou với phương trình \(u = \cos \left( {2\pi t + \dfrac{\pi }{2}} \right)\,\,\left( {mm} \right)\), trong đó t tính bằng s. Tính từ thời điểm ban đầu t = 0, thời điểm vị trí chính giữa trên màn quan sát có nháy sáng lần thứ 2021 là
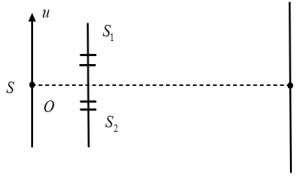
Trả lời bởi giáo viên
Khoảng vân giao thoa là:
\(i = \dfrac{{\lambda D}}{a} = \dfrac{{{{500.10}^{ - 9}}.2}}{{{{1.10}^{ - 3}}}} = {1.10^{ - 3}}\,\,\left( m \right) = 1\,\,\left( {mm} \right)\)
Điểm chính giữa trên màn I có nháy sáng khi tại đó có vân sáng
Độ dịch chuyển cực đại của vân trung tâm trên màn là:
\({y_{\max }} = \dfrac{{D.{x_{\max }}}}{d} = \dfrac{{{{2.1.10}^{ - 3}}}}{{0,5}} = {4.10^{ - 3}}\,\,\left( m \right) = 4\,\,\left( {mm} \right) = 4i\)
→ trong \(\dfrac{1}{4}\) chu kì điểm sáng S dịch chuyển từ vị trí cân bằng đến biên, tại điểm I có 4 lần tạo vân sáng
→ trong 1 chu kì, tại điểm I có vân sáng 16 lần
Chu kì dao động của điểm sáng S là:
\(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{2\pi }} = 1\,\,\left( s \right)\)
Thời điểm ban đầu điểm sáng S ở vị trí cân bằng, điểm I có nháy sáng lần đầu tiên
Điểm I có nháy sáng lần thứ 2021 khi điểm sáng S thực hiện số chu kì là:
\(n = \dfrac{{2021 - 1}}{{16}} = 126,25 \Rightarrow t = nT = 126,25\,\,\left( s \right)\)
Hướng dẫn giải:
Điểm chính giữa trên màn có nháy sáng khi tại đó là vân sáng
Khoảng vân: \(i = \dfrac{{\lambda D}}{a}\)
Dịch chuyển màn một đoạn x theo phương thẳng đứng, vân sáng trung tâm dịch chuyển một đoạn: \(\left| y \right| = \dfrac{{Dx}}{d}\)
Chu kì dao động: \(T = \dfrac{{2\pi }}{\omega }\)

