Câu hỏi:
2 năm trước
OA, OB là hai đoạn dây dẫn thẳng, ACB và OBD là hai dây dẫn hình nửa đường tròn đường kính AB và OB. Các đoạn dây dẫn này đồng tính và cùng tiết diện. Biết điện trở của OA và OB bằng nhau và bằng R. Tính điện trở giữa A và B (RAB )
Trả lời bởi giáo viên
Đáp án đúng: a
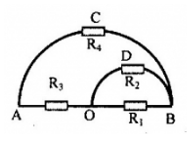
Gọi R1 = ROB = R, R2 = RODB, R3 = RAO = R, R4 = RACB
Từ hình vẽ, ta có:
((R1 // R2 ) nối tiếp R3 ) // R4
Ta có, dây dẫn tiết diện đều, đồng tính và điện trở của dây dẫn được xác định bằng biểu thức:
\(R = \rho \frac{l}{S}\)
\( \to \frac{{{R_2}}}{{{R_1}}} = \frac{{{l_2}}}{{{l_1}}} = \frac{{\pi \left( {\frac{{OB}}{2}} \right)}}{{OB}} \to {R_2} = \frac{{\pi R}}{2}\)
Ta có: R4 = 2R2 => R4 = πR
+ R1//R2 :
\({R_{12}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{{\frac{{\pi R}}{2}\pi R}}{{\frac{{\pi R}}{2} + \pi R}} = \frac{{\pi R}}{{\pi + 2}}\)
+ R12 nt R3:
\({R_{123}} = {R_{12}} + {R_3} = {R_{12}} = \frac{{\pi R}}{{\pi + 2}} + R = 2R\left( {\frac{{\pi + 1}}{{\pi + 2}}} \right)\)
+ R123 // R4:
\({R_{AB}} = \frac{{{R_{123}}{R_4}}}{{{R_{123}} + {R_4}}} = 2\pi R\left( {\frac{{\pi + 1}}{{{\pi ^2} + 4\pi + 2}}} \right) \approx 1,065R\)
Hướng dẫn giải:
+ Áp dụng biểu thức xác định điện trở của dây dẫn: \(R = \rho \frac{l}{S}\)
+ Áp dụng tính điện trở tổng cộng
Câu hỏi khác
- Đề kiểm tra giữa học kì 2 - đề số 1 Lý 11 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 4 Lý 11 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 1 Lý 11 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 05 Lý 11 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 04 Lý 11 có lời giải chi tiết
