Ở Việt Nam, phổ biến loại sáo trúc có 6 lỗ bấm, 1 lỗ thổi và một lỗ định âm (là lỗ để sáo phát ra âm cơ bản). Các lỗ bấm đánh số 1, 2, 3, 4, 5, 6 tính từ lỗ định âm; các lỗ này phát ra các âm có tần số cách âm cơ bản được tính bằng cung theo thứ tự: 1 cung; 2 cung; 2,5 cung; 3,5 cung; 4,5 cung; 5,5 cung. Coi rằng mỗi lỗ bấm là một ống sáo rút ngắn. Hai lỗ cách nhau một cung và nửa cung (tính từ lỗ định âm) thì có tỉ số chiều dài đến lỗ thổi tương ứng là \(\frac{8}{9}\) và \(\frac{15}{16}\). Giữa chiều dài L, từ lỗ thổi đến lỗ thứ i và tần số \({{f}_{i~}}\,\left( i=1\to 6 \right)\)của âm phát ra từ lỗ đó tuân theo công thức \(L=\frac{v}{2.{{f}_{i}}}\) (v là tốc độ truyền âm trong khí bằng 340 m/s). Một ống sáo phát ra âm cơ bản có tần số \({{f}_{0}}=440Hz\). Lỗ thứ 5 phát ra âm cơ bản có tần số:

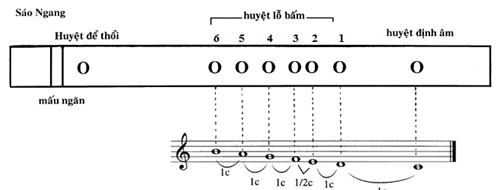
Hình ảnh mô tả sáo trúc:

+ Tần số âm cơ bản: \({{f}_{0}}=440Hz\)

+ Với L_i là chiều dài từ lỗ thổi đến lỗ thứ i.

→ Lỗ thứ nhất cách lỗ định âm một cung: \(\frac{{{L}_{1}}}{{{L}_{0}}}=\frac{8}{9}\)

→ Lỗ thứ nhất và lỗ thứ hai cách nhau một cung: \(\frac{{{L}_{2}}}{{{L}_{1}}}=\frac{8}{9}\)

→ Lỗ thứ ba cách lỗ thứ hai nửa cung: \(\frac{{{L}_{3}}}{{{L}_{2}}}=\frac{15}{16}\)

→ Lỗ thứ tư cách lỗ thứ ba một cung: \(\frac{{{L}_{4}}}{{{L}_{3}}}=\frac{8}{9}\)

→ Lỗ thứ năm cách lỗ thứ tư một cung: \(\frac{{{L}_{5}}}{{{L}_{4}}}=\frac{8}{9}\)

+ Từ các tỉ số trên ta có:

\(\frac{{{L}_{1}}}{{{L}_{0}}}.\frac{{{L}_{2}}}{{{L}_{1}}}.\frac{{{L}_{3}}}{{{L}_{2}}}.\frac{{{L}_{4}}}{{{L}_{3}}}.\frac{{{L}_{5}}}{{{L}_{4}}}=\frac{8}{9}.\frac{8}{9}.\frac{15}{16}.\frac{8}{9}.\frac{8}{9}\Leftrightarrow \frac{{{L}_{5}}}{{{L}_{0}}}=\frac{1280}{2187}\)

Mặt khác: 

\(\begin{gathered}
L = \frac{v}{{2.{f_i}}} \Rightarrow \left\{ \begin{gathered}
{L_0} = \frac{v}{{2.{f_0}}} \hfill \\
{L_5} = \frac{v}{{2.{f_5}}} \hfill \\
\end{gathered} \right. \Rightarrow \frac{{{L_5}}}{{{L_0}}} = \frac{{{f_0}}}{{{f_5}}} \hfill \\
\Rightarrow {f_5} = \frac{{{L_0}}}{{{L_5}}}.{f_0} = \frac{{2187}}{{1280}}.440 = 751,8Hz \hfill \\
\end{gathered} \)