Một vật chuyển động tròn đều xung quanh điểm \(O\) với đường kính \(50\,\,cm\) được gắn một thiết bị thu âm. Hình chiếu của vật này lên trục \(Ox\) đi qua tâm của đường tròn chuyển động với phương trình \(x = Acos\left( {10t + \varphi } \right)\). Một nguồn phát âm đẳng hướng đặt tại điểm \(H\) trên trục \(Ox\) và cách \(O\) một khoảng \(100\,\,cm\). Tại thời điểm \(t = 0\), mức cường độ âm đo được có giá trị nhỏ nhất và bằng \(50\,\,dB\). Tại thời điểm mà hình chiếu của vật đạt tốc độ \(1,25\sqrt 3 \,\,m/s\) lần thứ \(2021\) thì mức cường độ âm đo được có giá trị gần với giá trị nào nhất sau đây?
Trả lời bởi giáo viên
Hình chiếu của vật này lên trục \(Ox\) có biên độ là:
\(A = \frac{d}{2} = 25\,\,\left( {cm} \right) = 0,25\,\,\left( m \right)\)
Ở thời điểm đầu, mức cường độ âm đo được là nhỏ nhất:
\({L_{\min }} \Rightarrow {I_{\min }} \Rightarrow {r_{\max }} = 1,25\,\,\left( m \right) \to \) vật ở vị trí biên xa nhất so với điểm \(H\)
Áp dụng công thức độc lập với thời gian, ta có:
\({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2} \Rightarrow {x^2} + \frac{{{{\left( {1,25\sqrt 3 } \right)}^2}}}{{{{10}^2}}} = 0,{25^2} \Rightarrow x = \pm 0,125\,\,\left( m \right)\)
Trong một chu kì, có \(4\) lần vật đạt tốc độ \(1,25\sqrt 3 \,\,m/s\)
Ta có vòng tròn lượng giác:
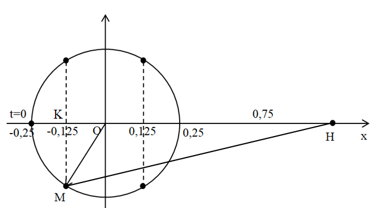
Từ vòng tròn lượng giác ta thấy vật có tốc độ \(1,25\sqrt 3 \,\,m/s\) lần thứ \(2021\) khi vật đi qua li độ \( - 0,125\,\,m\)
Khoảng cách từ điểm \(M\) tới điểm \(H\) là:
\(\begin{array}{l}r = MH = \sqrt {M{K^2} + K{H^2}} = \sqrt {\left( {O{M^2} - O{K^2}} \right) + {{\left( {OH + OK} \right)}^2}} \\ \Rightarrow r = \sqrt {\left( {0,{{25}^2} - 0,{{125}^2}} \right) + {{\left( {1 + 0,125} \right)}^2}} \approx 1,1456\,\,\left( m \right)\end{array}\)
Ta có hiệu mức cường độ âm:
\(\begin{array}{l}L - {L_{\min }} = \lg \frac{I}{{{I_{\min }}}} = \lg \frac{{{r_{\max }}^2}}{{{r^2}}}\\ \Rightarrow L - 5 = \lg \frac{{1,{{25}^2}}}{{1,{{1456}^2}}} \Rightarrow L \approx 5,076\,\,\left( B \right) = 50,76\,\,\left( {dB} \right)\end{array}\)
Cường độ âm có giá trị gần nhất với giá trị \(50,8\,\,dB\)
Hướng dẫn giải:
Hình chiếu của chuyển động tròn đều lên đường kính là dao động điều hòa có biên độ \(A = R = \frac{d}{2}\)
Công thức độc lập với thời gian: \({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2}\)
Sử dụng vòng tròn lượng giác
Cường độ âm: \(I = \frac{P}{{4\pi {r^2}}}\)
Hiệu hai mức cường độ âm: \({L_2} - {L_1} = \lg \frac{{{I_2}}}{{{I_1}}}\)
Câu hỏi khác
- Đề thi thử khoa học tự nhiên - lần 1 Tự chọn Đánh giá năng lực có lời giải chi tiết
- Đề thi thử khoa học tự nhiên - đhbk - lần 2 Tự chọn Đánh giá năng lực có lời giải chi tiết
- Đề thi thử khoa học tự nhiên - đề số 1 Tự chọn Đánh giá tư duy đại học Bách Khoa Hà Nội có lời giải chi tiết
- Đề thi thử khoa học tự nhiên - đề số 2 Tự chọn Đánh giá tư duy đại học Bách khoa Hà Nộicó lời giải chi tiết
- Đề thi khoa học tự nhiên - đề số 4 Tự chọn Đánh giá năng lực có lời giải chi tiết
