Một tụ điện có điện dung \(C = 0,202\mu {\rm{F}}\) được tích điện đến hiệu điện thế \({U_0}\). Lúc \(t = 0\), hai đầu tụ được đấu vào hai đầu của một cuộn dây có độ tự cảm bằng \(0,5H\). Bỏ qua điện trở thuần của cuộn dây và của dây nối. Lần thứ hai điện tích trên tụ bằng một nửa điện tích lúc đầu là ở thời điểm nào?
Trả lời bởi giáo viên
Thời điểm ban đầu, tụ được nạp đầy điện và bắt đầu phóng điện, điện tích trên tụ giảm dần.
Ta có biểu thức: \(q = {Q_0}.\cos \left( {\omega t} \right)\)
Chu kì dao động của mạch:
\(T = 2\pi \sqrt {LC} = 2\pi \sqrt {0,{{202.10}^{ - 6}}.0,5} = {2.10^{ - 3}}s\)
Biểu diễn trên VTLG:
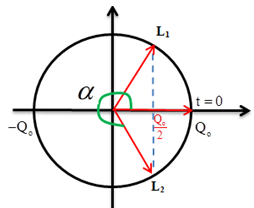
Góc quét tương ứng: \(\alpha = 2\pi - \dfrac{\pi }{3} = \dfrac{{5\pi }}{3}\)
\( \Rightarrow \) Lần thứ hai điện tích trên tụ bằng một nửa điện tích lúc đầu là:
\(t = \dfrac{\alpha }{\omega } = \alpha .\dfrac{T}{{2\pi }} = \dfrac{{5\pi }}{3}.\dfrac{{{{2.10}^{ - 3}}}}{{2\pi }} = \dfrac{1}{{600}}s\)
Hướng dẫn giải:
Điện tích trên hai bản tụ điện có biểu thức: \(q = {Q_0}.\cos \left( {\omega t + \varphi } \right)\)
Chu kì T được xác định bởi công thức: \(T = 2\pi \sqrt {LC} \)
Sử dụng VTLG và công thức tính thời gian: \(t = \dfrac{\alpha }{\omega } = \alpha .\dfrac{T}{{2\pi }}\)

