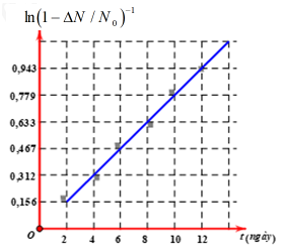
Một nhà vật lý hạt nhân làm thí nghiệm xác định chu kỳ bán rã \(\left( T \right)\) của một chất phóng xạ bằng cách dùng máy đếm xung để đo tỉ lệ giữa số hạt bị phân rã \(\left( {\Delta N} \right)\) và số hạt ban đầu \(\left( {{N_0}} \right)\). Dựa vào kết quả thực nghiệm đo được trên hình vẽ, hãy tính \(T\)?
Trả lời bởi giáo viên
Ta có: \({\left( {1 - \dfrac{{\Delta N}}{{{N_0}}}} \right)^{ - 1}} = \dfrac{1}{{1 - \dfrac{{\Delta N}}{{{N_0}}}}} = \dfrac{1}{{1 - \left( {1 - {2^{ - \dfrac{t}{T}}}} \right)}} = \dfrac{1}{{{2^{ - \dfrac{t}{T}}}}} = {2^{\dfrac{t}{T}}}\)
\( \Rightarrow \ln {\left( {1 - \dfrac{{\Delta N}}{{{N_0}}}} \right)^{ - 1}} = \ln \left( {{2^{\dfrac{t}{T}}}} \right)\)
Từ đồ thị ta thấy:
\(\left\{ \begin{array}{l}t = 6ngay\\\ln {\left( {1 - \dfrac{{\Delta N}}{{{N_0}}}} \right)^{ - 1}} = 0,467\end{array} \right. \Rightarrow \ln \left( {{2^{\dfrac{6}{T}}}} \right) = 0,467 \Rightarrow T = 8,9ngay\)
Hướng dẫn giải:
Số hạt nhân bị phân rã: \(\Delta N = {N_0}\left( {1 - {2^{ - \dfrac{t}{T}}}} \right)\)
Câu hỏi khác
- Đề thi giải quyết vấn đề - đề số 1 Giải quyết vấn đề Đánh giá năng lực Đại học Quốc gia thành phố Hồ Chí Minh có lời giải chi tiết
- Đề thi giải quyết vấn đề - đề số 7 Giải quyết vấn đề Đánh giá năng lực Đại học Quốc gia thành phố Hồ Chí Minh có lời giải chi tiết
- Đề thi giải quyết vấn đề - đề số 2 Giải quyết vấn đề Đánh giá năng lực Đại học Quốc gia thành phố Hồ Chí Minh có lời giải chi tiết
- Đề thi giải quyết vấn đề - đề số 6 Giải quyết vấn đề Đánh giá năng lực Đại học Quốc gia thành phố Hồ Chí Minh có lời giải chi tiết
- Đề thi giải quyết vấn đề - đề số 3 Giải quyết vấn đề Đánh giá năng lực Đại học Quốc gia thành phố Hồ Chí Minh có lời giải chi tiết
