Câu hỏi:
2 năm trước
Một điểm sáng S đặt trước một gương phẳng OM như hình:
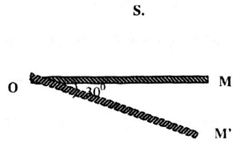
Khi cho gương quay một góc \(\alpha = {20^0}\) quanh O thì ảnh của S di chuyển, Đoạn đường OS’ quay được một góc bằng bao nhiêu?
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có:
Gọi \(S'\) là ảnh của \(S\) qua gương lúc đầu và \(S''\) là ảnh của \(S\) qua gương sau khi quay gương một góc \(\alpha = {20^0}\)
Như vậy, khi cho gương quay một góc \(\alpha \) quanh O thì ảnh S di chuyển trên cung \(S'S''\) bán kính bằng OS và đoạn đường OS’ quay được một góc x như hình
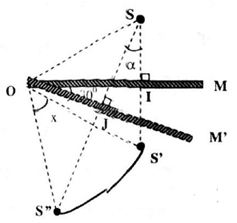
Do tính đối xứng của ảnh với vật qua gương nên \({\rm{OS}}'' = {\rm{OS = OS'}}\)
Hay nói cách khác \(S'',S'\) và \(S\) nằm trên cùng vòng tròn tâm O, bán kính \({\rm{OS}}\)
Như vậy góc \(\alpha \) là góc nội tiếp trong vòng tròn tâm O, có x là góc ở tâm cùng chắn cung \(S'S''\)
Do đó: \(x = 2\alpha \)
=> Đoạn đường \({\rm{OS}}'\) quay được một góc bằng: \(x = 2\alpha = 2.20 = {40^0}\)
Hướng dẫn giải:
+ Vẽ ảnh của điểm sáng trước và sau khi quay gương: Lấy đối xứng qua gương
+ Xác định góc quay của ảnh
Câu hỏi khác
- Đề kiểm tra giữa học kì 1 - đề số 01 Lý 7 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 01 Lý 7 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 02 Lý 7 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 03 Lý 7 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 02 Lý 7 có lời giải chi tiết
