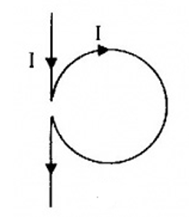
Một dây dẫn rất dài được căng thẳng, trong đó có một đoạn nhỏ được uốn thành vòng tròn bán kính 1,5cm (như hình dưới). Cho dòng điện cường độ \(I = 3A\) chạy trong dây dẫn. Xác định véc tơ cảm ứng từ tại tâm O của vòng dây.
Trả lời bởi giáo viên
+ Gọi \(\overrightarrow {{B_1}} ,\overrightarrow {{B_2}} \) lần lượt là cảm ứng từ gây bởi phần dòng điện thẳng dài và phần dòng điện tròn tại tâm O
+ Dựa vào quy tắc nắm bàn tay phải, ta suy ra véc tơ \(\overrightarrow {{B_1}} \) có chiều từ trong ra, véc tơ \(\overrightarrow {{B_2}} \) có chiều hướng vào trong
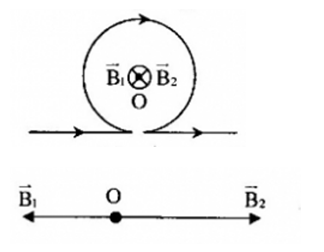
Ta có: \(\left\{ \begin{array}{l}{B_1} = {2.10^{ - 7}}\dfrac{I}{R}\\{B_2} = 2\pi {.10^{ - 7}}\dfrac{I}{R}\end{array} \right.\)
Cảm ứng từ tổng hợp tại O: \(\overrightarrow B = \overrightarrow {{B_1}} + \overrightarrow {{B_2}} \)
Vì \(\overrightarrow {{B_1}} \uparrow \downarrow \overrightarrow {{B_2}} \Rightarrow B = \left| {{B_1} - {B_2}} \right|\)
Ta có \({B_2} > {B_1} \Rightarrow \overrightarrow B \) có chiều là chiều của \(\overrightarrow {{B_2}} \) và có độ lớn:
\(\begin{array}{l}B = {B_2} - {B_1} = {2.10^{ - 7}}\dfrac{I}{R}\left( {\pi - 1} \right)\\ = {2.10^{ - 7}}\dfrac{3}{{1,{{5.10}^{ - 2}}}}\left( {\pi - 1} \right)\\ \approx 8,{57.10^{ - 5}}T\end{array}\)
Hướng dẫn giải:
+ Áp dụng các bước giải xác định cảm ứng từ (Xem lí thuyết phần V)
+ Áp dụng biểu thức xác định cảm ứng từ của dòng điện tròn: \(B = 2\pi {.10^{ - 7}}\dfrac{I}{R}\)
+ Áp dụng biểu thức xác định cảm ứng từ của dòng điện thẳng: \(B = {2.10^{ - 7}}\dfrac{I}{r}\)

