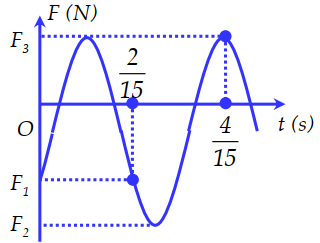
Một con lắc lò xo gồm một vật nhỏ có khối lượng \(200 g\) và lò xo có độ cứng \(k\), đang dao động điều hòa theo phương thẳng đứng. Chọn gốc tọa độ ở vị trí cân bằng, chiều dương hướng xuống. Hình trên là đồ thị biểu diễn sự phụ thuộc của lực đàn hồi \(F\) tác dụng lên vật theo thời gian \(t\). Biết \({F_1} + 3{F_2} + 6{F_3} = 0\). Lấy \(g =10 m/s^2\). Tại \(t = 0\), độ lớn của lực đàn hồi tác dụng lên vật có giá trị gần nhất với giá trị nào sau đây ?
Trả lời bởi giáo viên
Lực đàn hồi của lò xo được xác định bằng công thức: \(F = - k(\Delta {\ell _0} + x)\)
+ Ta có: (1)
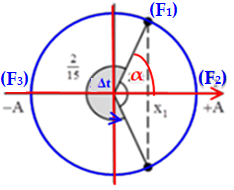
+ Từ đồ thị: à \(T = \dfrac{4}{{15}} - \dfrac{1}{2}\Delta t = \dfrac{1}{5}(s) \to \omega = 10\pi (rad/s) \to \alpha = \dfrac{{2\pi - \omega .\Delta t}}{2} = \dfrac{\pi }{3} \to {x_1} = \dfrac{A}{2}\) (2)
+ Từ (1) và (2) => \(A = 4\Delta {\ell _0} \to {x_1} = \dfrac{A}{2} = 2\Delta {\ell _0}\).
+ Tại t = 0: \({F_1} = - {k_1}(\Delta {\ell _0} + {x_1}) = - k.3\Delta {\ell _0} = - 3mg = - 3.0,2.10 = - 6(N)\). à Độ lớn: \(\left| {{F_1}} \right| = \)\(6(N)\)
Hướng dẫn giải:
Lực đàn hồi của lò xo được xác định bằng công thức: \(F = - k(\Delta {\ell _0} + x)\)
Với \(\Delta {\ell _0}\) là độ biến dạng của lò xo tại vị trí cân bằng, x là li độ của vật (chiều dương hướng xuống!).

