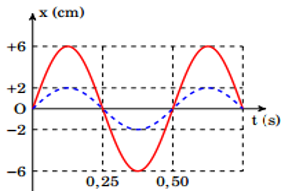
Hai con lắc lò xo giống nhau có cùng khối lượng vật nặng m và cùng độ cứng lò xo k. Hai con lắc dao động trên hai đường thẳng song song, có vị trí cân bằng ở cùng gốc tọa độ. Chọn mốc thế năng tại vị trí cân bằng, đồ thị li độ - thời gian của hai dao động được cho như hình vẽ (con lắc thứ hai có biên độ nhỏ hơn con lắc thứ nhất ). Ở thời điểm t, con lắc thứ nhất có vận tốc 72cm/s và con lắc thứ hai có thế năng \({4.10^{ - 3}}J\). Lấy \({\pi ^2} = 10\). Khối lượng m là:

Khi chiếu chùm tia tử ngoại vào một ống nghiệm đựng dung dịch fluorexêin thì thấy dung dịch phát ra ánh sáng màu lục. Đó là hiện tượng:

Một lượng chất phóng xạ có khối lượng ban đầu là \({m_0}\). Sau 4 chu kỳ bán rã khối lượng chất phóng xạ còn lại là

Phát biểu nào sau đây là không đúng?

Máy phát điện xoay chiều một pha có phần cảm gồm p cặp cực (p cực nam và p cực bắc). Khi máy hoạt động, rôto quay đều với tốc độ n vòng/giây. Suất điện động do máy tạo ra có tần số là

Lưỡng cực điện xảy ra khi các điện tích dương và âm (ví dụ một proton và một điện tử hoặc một cation và một anion) tách rời khỏi nhau và cách nhau một khoảng không đổi. Một phân tử hoạt động như một lưỡng cực điện chuyển động theo phương ngang với vận tốc không đổi vào điện trường đều theo phương thẳng đứng (như hình vẽ). Các điện tích âm và dương của phân tử đi vào điện trường cùng một lúc. Phát biểu nào sau đây là đúng về vận tốc của phân tử trong điện trường?

Vệ tinh địa tĩnh là vệ tinh mà ta quan sát nó từ Trái Đất dường như nó đứng im trên không. Điều kiện để có vệ tinh địa tĩnh là phải phóng vệ tinh sao cho mặt phẳng quay của nó nằm trong mặt phẳng xích đạo của Trái Đất, chiều chuyển động theo chiều quay của Trái Đất và có chu kì quay đúng bằng chu kì tự quay của Trái Đất là 24 giờ.Cho bán kính Trái Đất R = 6400 km. Biết vệ tinh quay trên quỹ đạo với tốc độ dài 3,68 km/s. Khi vệ tinh phát sóng điện tử, tỉ số giữa thời gian dài nhất và ngắn nhất sóng đến được mặt đất là: