Điện năng được truyền từ trạm phát điện đến nơi tiêu thụ bằng đường dây tải điện một pha. Ban đầu hiệu suất truyền tải là 80%. Cho công suất truyền đi không đổi và hệ số công suất ở nơi tiêu thụ (cuối đường dây tải điện) luôn bằng 0,8. Để giảm hao phí trên đường dây 4 lần thì cần phải tăng điện áp hiệu dụng ở trạm phát điện lên n lần. Giá trị của n là

+ Ta có:

 \(\dfrac{{\Delta {P_1}}}{{\Delta {P_2}}} = \dfrac{{I_1^2R}}{{I_2^2R}} = 4 \Rightarrow {I_2} = \dfrac{{{I_1}}}{2} \Rightarrow \Delta {U_2} = \dfrac{{\Delta {U_1}}}{2}\) 

+ Chuẩn hóa: Chọn ΔU₁ =1(V).

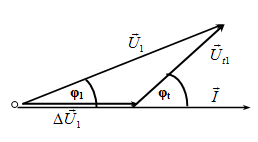
\({H_1} = 0,8 \Rightarrow \left\{ \begin{array}{l}{P_{{t_1}}} = 0,8P\\\Delta {P_1} = 0,2P\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}{U_{{t_1}}}cos{\varphi _t} = 0,8{U_1}cos{\varphi _1}\\\Delta {U_1} = 0,2{U_1}cos{\varphi _1}\end{array} \right.\)

\( \Leftrightarrow \frac{{{U_{{t_1}}}}}{{\Delta {U_1}}} = 5\xrightarrow{{\Delta {U_1} = 1}}{U_{{t_1}}} = 5V\)

\(\Rightarrow {U_1} = \sqrt {U_{t1}^2 + {{(\Delta {U_1})}^2} + 2{U_{t1}}\Delta {U_1}\cos {\varphi _t}}  = \)\(\sqrt {34}(V) \)

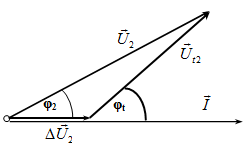
\(\begin{array}{l}{H_2} = 0,95 \Rightarrow \left\{ \begin{array}{l}{P_{t1}} = 0,95P\\\Delta {P_1} = 0,05P\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{U_{t2}}\cos {\varphi _t} = 0,95{U_2}\cos {\varphi _2}\\\Delta {U_2} = 0,05.{U_2}\cos {\varphi _2}\end{array} \right.\end{array}\)

\( \Leftrightarrow \dfrac{{{U_{t2}}}}{{\Delta {U_2}}} = 23,75\xrightarrow{{\Delta {U_2} = 0,5}}{U_{t2}} = 11,875(V)\)

\( \Rightarrow{U_2} = \sqrt {U_{t2}^2 + {{(\Delta {U_{21}})}^2} + 2{U_{t2}}\Delta {U_2}\cos {\varphi _t}}  \approx 12,2787(V)\)

+ Giá trị của n là: \(n = \dfrac{{{U_2}}}{{{U_1}}} \approx \dfrac{{12,2787}}{{\sqrt {34} }} \approx \)\(2,1058\)