Câu hỏi:
2 năm trước
Vật dao động điều hòa có đồ thị a – t như hình vẽ.
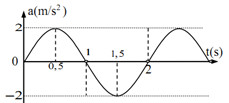
Quãng đường vật đi được trong 1 chu kì là bao nhiêu? Lấy \({\pi ^2} = 10\)
Trả lời bởi giáo viên
Đáp án đúng: c
Từ đồ thị, ta có:
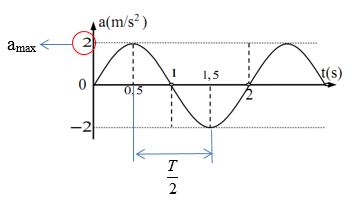
+ \(\Delta t = 1,5 - 0,5 = \dfrac{T}{2} \to T = 2s\)
=> Tần số góc: \(\omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{2} = \pi \left( {rad/s} \right)\)
+ Gia tốc cực đại: \({a_{max}} = {\omega ^2}A = 2m/{s^2}\)
=> Biên độ dao động: \(A = \dfrac{{{a_{max}}}}{{{\omega ^2}}} = \dfrac{2}{{{\pi ^2}}} = 0,2m\)
+ Quãng đường vật đi được trong 1 chu kì: \(S = 4A = 4.0,2 = 0,8m\)
Hướng dẫn giải:
+ Đọc đồ thị dao động
+ Sử dụng biểu thức tính tần số góc: \(\omega = \dfrac{{2\pi }}{T}\)
+ Vận dụng biểu thức tính gia tốc cực đại: \({a_{max}} = {\omega ^2}A\)
+ Quãng đường vật đi được trong 1 chu kì: \(S = 4A\)

